2.1. Углеродные нанотрубки
2.1.1. Описание структуры углеродных нанотрубок
2.1.1.1. Классификация углеродных нанотрубок
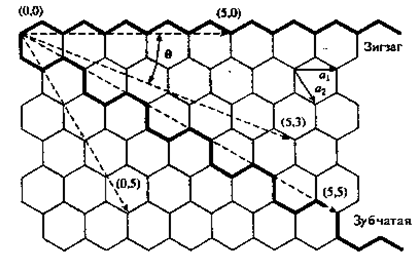
Идеальная нанотрубка представляет собой свернутую в цилиндр графитовую плоскость, т. е. поверхность, выложенную правильными шестиугольниками, в вершинах которых расположены атомы углерода. Результат такой операции зависит от угла ориентации графитовой плоскости относительно оси нанотрубки. Угол ориентации задает хиральность нанотрубки, которая определяет, в частности, ее электрические характеристики.
Рис. 2-1. Часть графитовой плоскости, свертывание которой в цилиндр приводит к образованию однослойной нанотрубки [12].
Структура нанотрубок описывается двумя целыми числами (m, n), указывающими координаты шестиугольника, который в результате сворачивания плоскости должен совпасть с шестиугольником, находящимся в начале координат. Некоторые из таких шестиугольников вместе с соответствующими обозначениями отмечены на рис. 2-1. Также эти числа можно обозначить как параметры так называемого хирального вектора, который задается следующей формулой:
(2.1) |
где
элементарные
векторы трансляций графитовой плоскости.
Другой способ обозначения хиральности состоит в указании угла между направлением сворачивания нанотрубки и направлением, в котором соседние шестиугольники имеют общую сторону.
Однослойные нанотрубки делятся на следующие подвиды: УНТ типа «armchair» (n, n), или «зубчатые»[1]; типа «zigzag» (n, 0), или «зигзагообразные»; хиральные (n, m), где n > m.
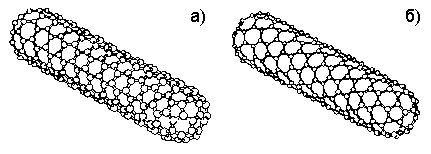
Структуры нанотрубок, отвечающие конфигурациям «зубчатая» и «зигзагообразная», показаны на рис. 2-2.
Рис. 2-2. Зубчатая (а) и зигзагообразная (б) нанотрубки [16].
Индексы хиральности однослойной нанотрубки (m, n) однозначным образом определяют ее диаметр D. Эта связь имеет следующий вид:
|
где d0 = 1,42 Å
расстояние
между соседними атомами углерода в графитовой плоскости. Связь между индексами
хиральности (m, n) и углом θ дается соотношением [15]:
|
Электронные и колебательные свойства УНТ существенным образом зависят от типа трубок.
Если разница |m
n| кратна 3, такие УНТ обладают
металлическими свойствами. Полуметаллами являются также все ахиральные трубки
типа «armchair». В других
случаях УНТ показывают полупроводниковые свойства [12].
2.1.1.2. Многослойные УНТ
Многослойные нанотрубки отличаются от однослойных значительно более широким разнообразием форм и конфигураций. Разнообразие структур проявляется как в продольном, так и в поперечном направлении.
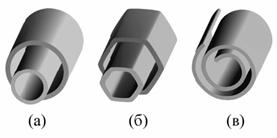
Рис. 2-3. Модели поперечных структур многослойных
нанотрубок: а
матрешка;
б
шестигранная призма; в
свиток
[17].
Возможные разновидности поперечной структуры многослойных нанотрубок представлены на рис. 2-3. Структура типа матрешки (russian dolls) (см. рис. 2-3, а) представляет собой совокупность коаксиально вложенных друг в друга однослойных цилиндрических нанотрубок. Другая разновидность этой структуры (см. рис. 2-3, б) представляет собой совокупность вложенных друг в друга коаксиальных призм. Наконец, последняя из приведенных структур (см. рис. 2-3, в) напоминает свиток (scroll). Для всех структур на рис. 2-3 характерно значение расстояния между соседними графитовыми слоями, близкое к величине 3,4 Å, присущей расстоянию между соседними плоскостями кристаллического графита.
Реализация той или иной структуры многослойной нанотрубки в конкретной экспериментальной ситуации зависит от условий синтеза. Анализ имеющихся экспериментальных данных указывает, что наиболее типичной структурой многослойных нанотрубок является структура типа матрешки (см. рис. 2-3, а), в которой трубки меньшего размера последовательно вложены в трубки большего размера [17].
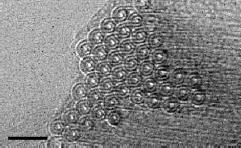
Следует заметить, что многослойные нанотрубки привлекают к себе не меньшее внимание, чем однослойные УНТ (ОУНТ). Так, например, недавно был разработан метод, позволяющий получить «бумагу», сплетенную из двухслойных углеродных нанотруб (рис. 2-4), с чистотой материала 95 % [18].
Рис. 2-4. Изображение «бумаги», состоящей из переплетенных двухслойных нанотруб. Масштаб: 5 нм [18].
2.1.1.3. Электронная структура углеродных нанотрубок
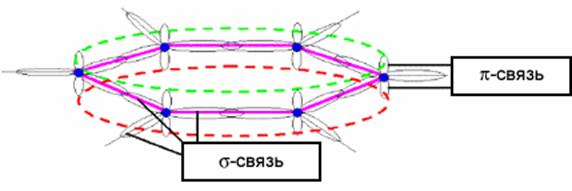
Рис. 2-5. Графитовый слой. Схематическое представление химической связи между атомами углерода [13].
Свойства углеродных нанотрубок, прежде всего, зависят от
природы химической связи между атомами углерода. Поскольку углеродная
нанотрубка может быть представлена как свернутый в цилиндр графитовый лист,
очевидно, что типы связей этих структур подобны. Конфигурация электронных
оболочек атома углерода
1s22s22p2. В графите
происходит sp2-гибридизация
электронных оболочек, т. е. объединение одной s-орбитали и двух p-орбиталей, дающее в результате три sp2-гибридизованные
орбитали, повернутые друг относительно друга на 120° в плоскости
(рис. 2-5). Лежащие в плоскости σ-связи отвечают
за сильное ковалентное связывание между атомами, в то время как π-связи, расположенные нормально,
за
слабое взаимодействие между слоями графита [13].
2.1.1.4. Зонная структура однослойных нанотрубок
Рассмотрим происхождение зонной структуры углеродных нанотрубок различной хиральности.
Хорошо известна формула дисперсии энергии связывающих и антисвязывающих π-зон для графита, рассчитанная методом сильной связи [14, 19]:
где t
интеграл
переноса, a
параметр
решетки (a = 2,46 Å).
На рис. 2-6 показана дисперсия энергии для первой зоны Бриллюэна. Видно,
что в точке K происходит вырождение энергии, определяющее свойства графита как полуметалла.
|
Рис. 2-6. Дисперсия энергии для графитового листа в первой зоне Бриллюэна. |
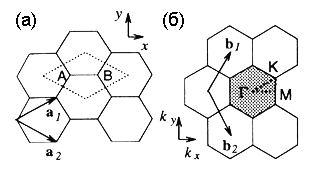
Рис. 2-7. элементарная ячейка (пунктир) (а) и первая зона Бриллюэна (область, закрашенная серым цветом) (б) для графитового листа [14]. |
Исходя из сравнения геометрических структур графита и УНТ,
можно видеть, что основное различие между ними
в
граничных условиях. Графитовая плоскость обычно рассматривается как бесконечно
протяженная, в то время как УНТ может быть рассмотрена подобным образом лишь в
направлении оси трубки. Следовательно, в направлении оси трубки, где
периодичные граничные условия такие же, как и в графите, волновой вектор будет
изменяться подобным образом, т. е. квазинепрерывно, в то время как
граничные условия цикличной волновой функции при обходе трубки по кругу дают
набор дискретных компонент волнового вектора.
Рассмотрим в качестве примера два типа нехиральных УНТ:
«зубчатый» и «зигзагообразный». В случае зубчатой углеродной нанотрубки
волновой вектор, связанный с обходом УНТ по кругу, будет направлен вдоль оси x (рис. 2-7). После
применения условия Борна
Кармана
можно получить для kx следующее выражение:
Подставив (2.5) в (2.4), получим зависимость энергии от волнового вектора для УНТ зубчатого типа:
где k параллелен вектору
(рис. 2-8, б).
При
(2.6) переходит в выражение
|
Таким образом, в этой точке происходит пересечение зон при
.
Важно, что оно не зависит от числа n, т. е. от диаметра зубчатой УНТ. Отсюда можно заключить,
что все УНТ типа (n, n) проявляют металлические
свойства. В качестве примера на рис. 2-8, в представлена зонная
картина для УНТ (5, 5).
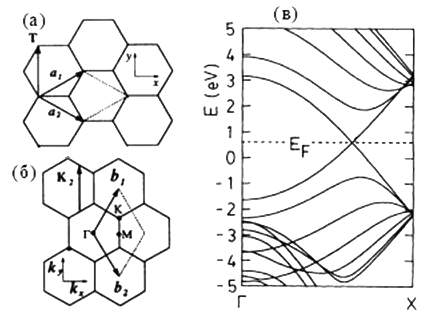
Рис. 2-8. Часть элементарной ячейки зубчатой УНТ (n, n) (а);
элементарные
векторы ячейки,
вектор
трансляций; первая зона Бриллюэна зубчатой УНТ (n, n) (б),
обратные
векторы ячейки; зонная структура ОУНТ (5, 5) (в). X
граница
зоны Бриллюэна [14, 20].
Рассмотрим «зигзагообразные» УНТ (n, 0). Волновым вектором, изменяющимся дискретно, будет ky,q:
а (2.4) переходит в следующее выражение:
В центре зоны Бриллюэна (
) (2.9) можно записать в виде
Таким образом, если
,
происходит пересечение зон. Следовательно, можно сделать вывод, что УНТ типа (n, 0) будут проявлять
металлические свойства, если n будет кратно трем, в любом другом случае «зигзагообразные» УНТ будут
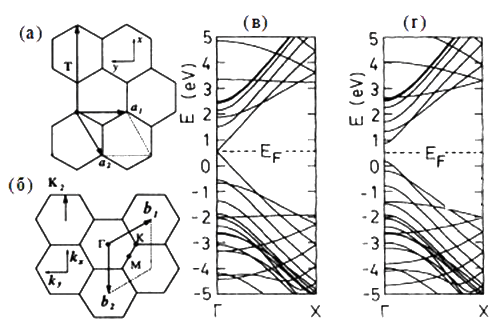
полупроводниками. Это подтверждают эксперимент и теоретические расчеты [21]. Для примера на рис. 2-9, в, г приведены
зонные структуры для УНТ (12, 0) и (13, 0) соответственно.
Рис. 2-9. Часть элементарной ячейки зигзагообразной УНТ (n, 0) (а); первая зона Бриллюэна зигзагообразной УНТ (n, 0) (б); зонная структура ОУНТ (12, 0) (в); зонная структура ОУНТ (13, 0) (г) [14, 20].
Хиральные нанотрубки могут быть также либо металлическими,
либо полупроводящими в зависимости от хирального угла и диаметра трубки. Дрессельхауз
(Dresselhaus) и ее
коллеги [16, 22] показали, что металлическая проводимость
возникает, когда разность индексов нанотрубки кратна трем. Таким образом, треть
хиральных труб являются металлическими, а две трети
полупроводящими.
Суммируя вышеприведенное обсуждение, можно сказать, что, как ожидается, все
зубчатые ОУНТ являются металлическими, тогда как одна треть зигзагообразных и
хиральных трубок должна быть также металлической, а остальные
полупроводящими
[16, 22, 23].
2.1.1.5. Группа симметрии однослойной УНТ
Однослойная УНТ хиральности (m, n) может быть представлена как
одномерный кристалл, характеризующийся вектором
,
направленным вдоль оси нанотрубки, длину которого можно найти из следующего
выражения:
(2.11) |
где
|
Величина с в (2.11) определяется из соотношения (2.1), d
это
наибольший общий множитель чисел n и m; r
любое
целое число. Количество атомов на элементарную ячейку задается величиной 2N, где
|
Для ОУНТ, определяемой индексами (n, m), цилиндр делится на d одинаковых частей, следовательно, к нанотрубке можно применить
операцию оси симметрии
-
вращение вокруг оси трубки на угол
.
Другая операция симметрии
это
винтовой поворот R = (ψ,τ ), угол ψ которого равен
(2.14) |
и сдвиг на вектор трансляции
вдоль направления оси трубки имеет значение
|
В (2.14) величина Ω определяется уравнением
|
где p и q
целые
числа, однозначно определяемые соотношениями
|
Для случая d=1
группа симметрии УНТ с индексами (n, m)
это
цикличная группа порядка N:
|
где E
единичный
элемент и
.
В общем случае, когда d > 1, цилиндр делится на d одинаковых частей, откуда
следует, что группа симметрии УНТ в общем случае определяется так:
|
где
|
и
|
Операция Сd есть вращение на угол
вокруг оси УНТ, а
.
Применяя вышеизложенные формулы для случая зубчатой и
зигзагообразных нанотрубок, видим, что они принадлежат группам симметрии
и
,
где
содержит две операции симметрии: единичную и
вращение на угол 2 π/2n вокруг оси трубки, следующего за трансляцией
.
Зубчатая и зигзагообразная нанотрубки, впрочем, имеют также и другие операции
симметрии, такие как операции инверсии и отражения в плоскостях, параллельных
оси трубки. Таким образом, бесконечно длинная, бездефектная нанотрубка принадлежит
группе симметрии:
|
Выбор между Dnd и Dnh определяется наличием операции инверсии в ОУНТ [24].