2.3. Метод упрощения расчетов однослойных нанотрубок

Теоретическое квантово-химическое исследование НТ является достаточно трудоемкой задачей, главным образом из-за времени счета, которое требуется для расчетов НТ больших диаметров, наиболее часто встречающихся в экспериментах. К примеру, элементарная ячейка типичных ОУНТ обычно содержит от 10¹ до 10² атомов, но при исследовании влияния дефектов (адсорбируемые молекулы, вакансии) на свойства ОУНТ необходимо рассматривать несколько элементарных ячеек, что приводит к минимальной длине рассматриваемого участка ОУНТ ~ 10 Å. При такой длине можно избежать нежелательного влияния дефектов в соседних ячейках друг на друга, т. е. считать дефекты изолированными. Таким образом, исследование дефектов любого вида внутри ОУНТ требует рассмотрения структуры, содержащей уже на порядок большее число атомов (~10² 10³), чем содержится в элементарной ячейке. На данный момент расчет электронной структуры подобных структур является чрезвычайно трудоемкой задачей для любого квантово-химического метода расчета (особенно ab initio), даже для тех методов, где явно используются периодичные условия теоремы Блоха (методы, базирующиеся на muffin tin разложении (LMTO, FPLMTO, LAPW и т. д.), метод псевдопотенциала и др.). Расчетное время названных методов изменяется пропорционально от N^~2 (здесь и далее N   число атомов в элементарной ячейке рассчитываемой структуры) до N⁴ (метод ЛКАО Хартри Фока). Согласно [29], одним из наиболее быстрых методов расчета является метод псевдопотенциала, использующий сверхмягкий псевдопотенциал Вандербильта, разложение по плоским волнам и итерационный метод диагонализации гамильтониана в рамках теории функционала плотности. В [29] было показано, что для систем, содержащих до 1000 электронов, расчетное время данного метода ~N². Но даже для данного метода можно предположить, что в исследованиях, связанных с расчетами НТ больших диаметров, эффективное уменьшение размера рассчитываемой ячейки и числа атомов в ней будет являться критически важным, если оно не будет приводить к существенной погрешности из-за трансформации ячейки.

2.3.1. Детали метода

Нами предложена методика, позволяющая значительно сократить время расчета электронной структуры НТ. Данное приближение, имеющее в основе изменение геометрии НТ, позволяет значительно уменьшить размер элементарной ячейки НТ, а также количество атомов в ней. Считая, что метод применяется для проведения расчетов в базисе плоских волн, в котором волновая функция рассчитывается, и в областях пространства, где она практически равна нулю, предложенный метод позволяет не рассчитывать электронную плотность вблизи оси НТ, где электронная плотность ρ   0, дополнительно увеличивая таким образом скорость расчета. Метод был применен для расчета некоторых однослойных углеродных ОУНТ, а также однослойной нитрид-борной нанотрубки (10, 10).

Основная идея метода базируется на том, что электронная структура ОУНТ и графитовой плоскости имеют схожие черты. Только в случае ОУНТ самых малых диаметров (D≤6Å) электронные структуры графита и ОУНТ начинают несколько различаться. Исходя из сравнения геометрических структур графитовой плоскости и ОУНТ, можно видеть, что основное различие между ними   в граничных условиях. Графитовая плоскость рассматривается как бесконечно протяженная, и граничные условия для волновых функций электрона в ней вводятся с помощью теоремы Блоха. При этом волновая функция электрона зависит от двумерного волнового вектора параллельного графитовой плоскости.

В случае же ОУНТ граничные условия схожи с граничными условиями для графита лишь в направлении оси трубки (ось Z).

Если рассматривать волновой вектор k_x вдоль свернутой графитовой поверхности и перпендикулярной к оси трубки, очевидно, что он изменяется дискретно благодаря периодичности при обходе вдоль окружности нанотрубки.

Данная периодичность геометрии нанотрубок позволила нам предложить возможность изменения геометрии рассчитываемой структуры путем разделения геометрической структуры нанотрубки на эквивалентные секторы и отражения каждого последующего сектора относительно плоскости, касательной к смежным секторам вдоль линии их соприкосновения.

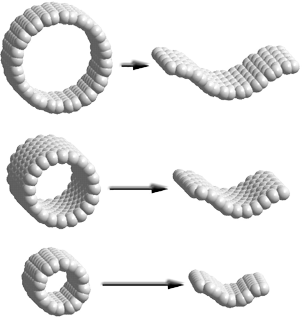
На рис. 2-22 показан пример такой последовательной трансформация ОУНТ в гофрированные поверхности (ГП), состоящие из двух и, далее, из четырех секторов, обладающих той же кривизной, что и первоначальная геометрическая структура ОУНТ.

Рис. 2-22. Последовательная трансформация секции нанотрубки в гофрированную поверхность.

При этом на рис. 2-22 изображены проекции нанотрубки и обеих ГП на плоскость, перпендикулярную оси нанотрубки. Там же показаны линии C_i C_i+1, являющиеся нормалями к плоскостям отражения секторов, с помощью отражения в которых и образуются ГП. Также показаны точки P_i, которые являются проекциями линий соприкосновения последовательных секторов. При рассмотрении последовательных трансформаций нанотрубки на первом этапе происходит трансформация исходной ОУНТ в простейшую ГП путем отражения половинного сектора нанотрубки относительно плоскости, проходящей через линию соединения (с проекцией P₁). Далее эта структура трансформируется в следующую ГП путем отражения предыдущей ГП уже относительно двух плоскостей (проходящих через линии с проекциями P₂, P₃). Далее процесс разбиения ГП может повторяться. При этом, если число плоскостей отражения равно M, то количество эквивалентных секций N соответствующей ГП, формируемой из структуры трубки, равно N = M + 1. На рис. 2-23 показан пример трансформации нанотруб различных хиральностей в соответствующие им гофрированные поверхности.

Рис. 2-23. Трансформация НТ различных типов в гофрированную поверхность.

Тот факт, что ОУНТ разбивается на некоторое количество периодически повторяемых секций, расположенных вдоль оси x, позволяет произвести расчет электронной структуры только для одной секции ГП. При увеличении степени разбиения нанотрубки происходит уменьшение элементарной ячейки ГП. При этом будет увеличиваться скорость расчетов.

Следует учитывать, что периодичность ГП вдоль оси X приводит к зависимости волновой функции электрона   от k_x. И если в случае нанотрубки волновой вектор k может изменяться только в одном измерении (вдоль оси трубки), то волновой вектор k для ГП имеет две размерности (k_x, k_z). При этом граничные условия (цикличность) для волновой функции при обходе трубки по кругу приводят к единственно возможному набору (L_x   период ГП вдоль координаты x).

Благодаря тому, что структура ГП отличается от ОУНТ только тем, что кривизна в ней изменяется скачкообразно (только по знаку) вдоль лишь небольшого числа линий с проекциями P_i, можно ожидать, что любая собственная волновая функция   электрона, распространяющегося вдоль ГП, будет близка к некоторой волновой функции электрона, распространяющегося вдоль поверхности соответствующей ОУНТ.

Необходимо отметить, что число атомов в элементарной ячейке ГП равняется числу атомов элементарной ячейки ОУНТ, деленному на N. При этом увеличение набора возможных величин квазиимпульса k_x в N раз восстанавливает полное число возможных электронных собственных состояний в нанотрубке.

Интересно отметить, какой выигрыш в скорости по сравнению с обычным расчетом для нанотрубок дает предложенное приближение. Считая, что в случае ОУНТ большого радиуса R выбираемый размер элементарной ячейки, определяемый L_x, L_y, будет гораздо больше, чем требуемый вакуумный промежуток между соседними трубками, и основываясь на рис. 2-22, можно легко вывести следующие соотношения:

(2.23)

Если учесть, что в данном методе скорость расчета V пропорциональна, как минимум, (N_atoms   число атомов в элементарной ячейке), а количество атомов в элементарной ячейке линейно зависит от ее объема, легко получить следующую формулу:

.

(2.24)

Для N >> π скорость расчета будет пропорциональна

.

(2.25)

Увеличение числа волновых векторов k_x в ГП компенсируется уменьшением числа атомов в ее элементарной ячейке.

2.3.2. Причина возможных погрешностей метода

Очень важно определить источник возможных погрешностей в расчете электронной структуры после трансформации УНТ-ГП. Очевидно, что он связан с локальным изменением кривизны рассматриваемой структуры. Именно кривизна искривленной графитовой плоскости ответственна за отличия (небольшие) электронной структуры нанотрубок по сравнению с электронной структурой графитового листа. Рассматривая гофрированную поверхность в цилиндрических координатах относительно осей вращения (см. проекции осей C_i на рис. 2-22), видно, что первая производная координат точки на поверхности ГП по углу поворота непрерывна, а величина кривизны, определяемая второй производной координат, обращается в ноль вдоль линий, проекциями которых на рис. 2-22 являются точки P_i. В остальных же точках гофрированной поверхности величина кривизны по модулю совпадает с кривизной ОУНТ. Иными словами, трансформация геометрической структуры нанотрубки в ГП с точки зрения решений уравнения Шредингера является корректной процедурой везде, за исключением линий соединения секторов (с проекциями P_i), которые одновременно принадлежат двум различным секторам ГП и где величина кривизны обращается в ноль.

Численно источник погрешности можно увидеть непосредственно из дифференциального уравнения Шредингера, расписывая оператор Лапласа в цилиндрических координатах:

(2.26)

Учитывая, что C₃P₁ =  C₂P₁, а также что первая и вторая производные в операторе Лапласа имеют разностные аппроксимации

(2.27)

становится очевидным, что все члены в лапласиане являются непрерывными функциями , за исключением члена , меняющего знак вдоль линий соединения P_i. Этот член и является единственной причиной возможных изменений в значении лапласиана при трансформации ОУНТ-ГП. К счастью, из формулы следует, что данный член уменьшается пропорционально увеличению радиуса НТ. Следовательно, если диаметр исходной нанотрубки достаточно велик, а число точек P_i невелико, можно ожидать, что электронная структура ГП будет практически совпадать с электронной структурой ОУНТ.

2.3.3. Результаты расчета электронной структуры ГП

В качестве примера были произведены расчеты электронной структуры ОУНТ различного диаметра и хиральности, а также соответствующих им ГП. Были рассчитаны зонная структура, плотность состояний и величины энергий связи для зигзагообразной однослойной углеродной нанотрубки (20, 0), а также для зубчатых ОУНТ (8, 8) и (16, 16).

Все расчеты были проведены с использованием программы VASP.

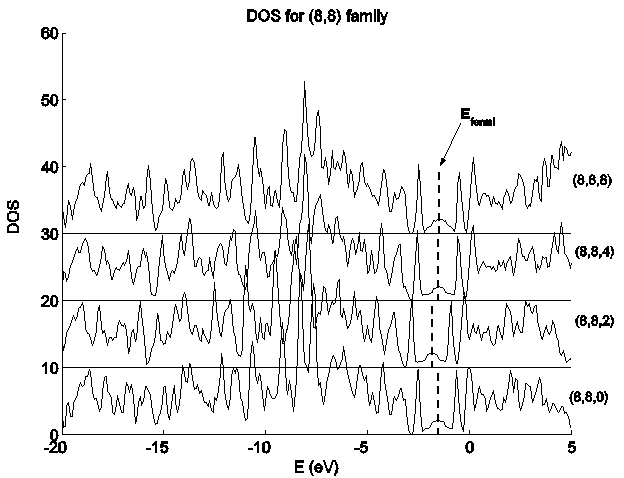
Рис. 2-24. Плотность состояний для структур (8, 8, i), i= {0, 2, 4, 8}.

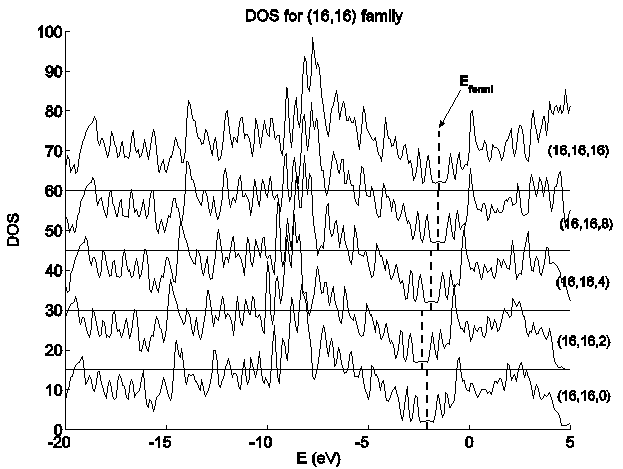
Рис. 2-25. Плотность состояний для структур (16, 16, i), i = {0, 2, 4, 8, 16}.

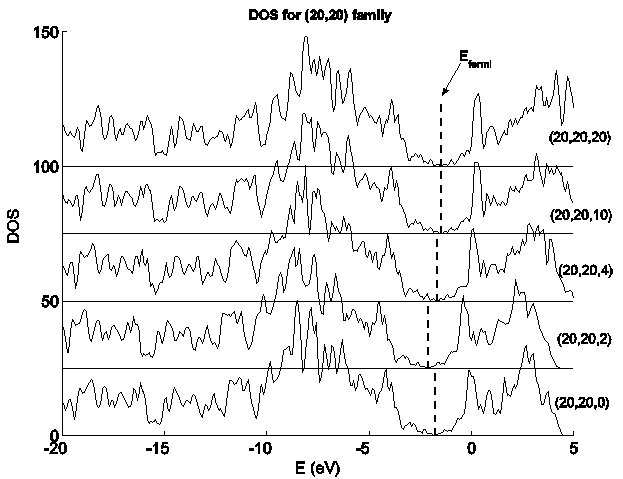
Рис. 2-26. Плотность состояний для структур (20, 0, i), i = {0, 2, 4, 10, 20}.

Все геометрические структуры однослойных углеродных нанотрубок и соответствующих им гофрированных поверхностей строились на основе графитовой плоскости, искривленной определенным образом. Плотности электронных состояний для всех исследуемых структур показаны на рис. 2-24 2-26. Гофрированные поверхности обозначаются на рисунках индексами (i, j, k), где k   количество частей, на которые делится нанотрубка при трансформации в ГП, а (i, j)   ее индексы хиральности. Например, (8, 8, 0)   это первоначальная ОУНТ (8, 8), а (8, 8, 4)   это ГП, полученная делением исходной нанотрубки на четыре части. Из рисунков видно, что плотность электронных состояний для всех гофрированных поверхностей практически совпадает с плотностью электронных состояний исходной нанотрубки, что говорит о несущественной роли конечного числа линий, где кривизна геометрических структур ОУНТ и ГП различается.

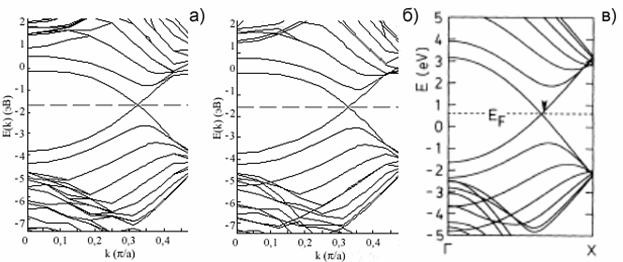
На рис. 2-27 изображены зонная структура для УНТ типа (8, 8) и соответствующая ей ГП, полученная из УНТ делением ее на четыре части. Из этого рисунка видно, что в зонной структуре УНТ и соответствующей ей ГП имеется пересечение зон и энергия Ферми располагается внутри разрешенной энергетической зоны, что говорит о проявлении этими структурами металлических свойств. Для сравнения на рис. 2-27, в показана зонная структура УНТ типа (12, 6), которая также проявляет металлические свойства [20].

Рис. 2-27. Рассчитанная зонная структура УНТ (8, 8) (а); зонная структура ГП (получена из УНТ путем деления на четыре части (8, 8, 4)) (б). Штриховой линией обозначена энергия Ферми. Для сравнения представлена зонная структура УНТ типа (6, 6), которая также проявляет металлические свойства [20] (в).

Также исследовано изменение электронной структуры всех структур в зависимости от оптимизации их геометрии. Для этого проведены расчеты для структур с оптимизированной и неоптимизированной геометрией. При оптимизации разрешались все степени свободы изменения координат атомов. Оптимизация проводилась методом самосопряженных градиентов. Структура считалась оптимизированной в случае, если абсолютная величина силы, действующей на любой атом, была меньше 0,02 эВ/Å. исследование показало, что DOS для всех оптимизированных структур практически совпадает с DOS для соответствующих неоптимизированных структур, поэтому на рисунках они не приведены.

Полная энергия связи (в расчете на атом) для всех структур (оптимизированных и неоптимизированных) показана в табл. 2-2. Также в таблице показаны данные о времени расчета одной итерации (по всем k-точкам), числе k-точек и числе плоских волн (усредненных по k-точкам). Расчет проводился на персональном компьютере PIII-860. Из таблицы видно, что энергия связи во всех ГП очень близка энергии связи соответствующих ОУНТ, при чем разница между этими энергиями увеличивается с увеличением разбиения трубки. Также видно, что во всех случаях энергия связи практически очень слабо зависит от оптимизации структуры.

Таблица 2-2. Энергия связи/атом (эВ) для структур (8, 8, i), (16, 16, i), (20, 0, i). Количество k-точек и плоских волн, длительность одной итерации при расчете структур
(8, 8, i) i = 0, 2, 4, 8 (оптимиз./неоптимиз.)	9,340	9,356	9,375	9,390	–
	9,331	9,340	9,347	9,364	–
(16, 16, i) i = 0, 2, 4, 8, 16 (оптимиз./неоптимиз.)	9,390	9,392	9,393	9,406	9,405
	9,381	9,348	9,381	9,385	9,389
(20, 0, i) i = 0, 2, 4, 10, 20 (оптимиз./неоптимиз.)	9,304	9,308	9,318	9,336	9,336
	9,304	9,307	9,310	9,321	9,331
Количество k-точек	14	28	42	84	154
Количество плоских волн	26290	15216	6290	2350	1158
Длительность одной итерации (сек)	88517	40037	12340	2500	890

 

2.3.4. Применение метода ГП для расчета упругих свойств углеродных и неуглеродных нанотрубок

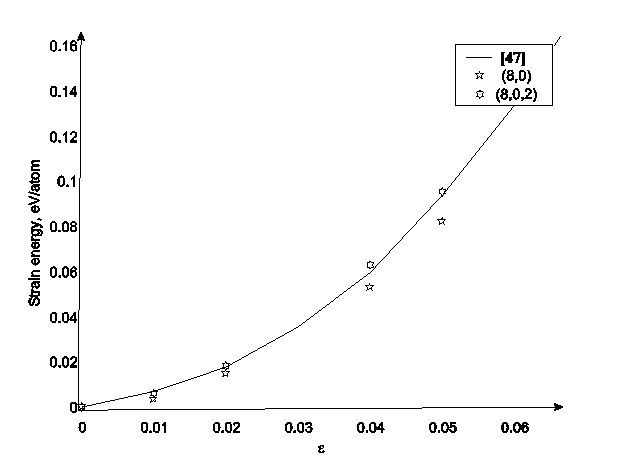
Предложенный метод также был применен для расчета упругих свойств углеродных и неуглеродных структур. рассчитаны модифицированные модули Юнга Y_s для ОУНТ (6, 6) и (10, 10) (табл. 2-3). Как видно из таблицы, в случае ОУНТ малого диаметра (6, 6) ошибка в вычислении Y_s для гофрированной структуры достаточно высока, но при увеличении диаметра нанотрубки точность вычисления растет в соответствии с результатами раздела 2.3.1. Кроме расчетов упругости зубчатых УНТ был произведен расчет энергии деформации (т. е. части энергии, связанной с искривлением графитового листа при образовании данной НТ) зигзагообразной ОУНТ (8, 0) и соответствующей ей ГП (8, 0, 2). Эти результаты приведены на рис. 2-28.

Рис. 2-28. Зависимость энергии деформации от ее величины для ОУНТ (8, 0) и соответствующей ГП (8, 0, 2).

Из рисунка видно, что энергии деформации исходной ОУНТ и соответствующей ей ГП очень близки (для умеренных деформаций), что говорит о возможности использования данной методики для расчета не только электронной структуры, но и упругих свойств УНТ.

Кроме расчетов свойств ОУНТ, также были проведены расчеты свойств ряда нанотрубок из нитрида бора (BN). рассчитана энергия связи для трубки (10, 10) и соответствующей ей ГП (10, 10, 2), а также значения модулей Юнга для этих структур (см. табл. 2-3). Видно, что предложенная методика с хорошей точностью описывает свойства и неуглеродных структур [48].

Таблица 2-3. Модуль Юнга Ys (TПа∙нм), рассчитанный для углеродных и неуглеродных структур
ОУНТ	Ys	ОУНТ	Ys	ОУНТ	Ys	BN-НТ	Ys
(6, 6)	0,463	(8, 0)	0,437	(10, 10)	0,423	(10, 10)	0,316
(6, 6, 2)	0,546	(8, 0, 2)	0,455	(10, 10, 2)	0,439	(10, 10, 2)	0,329
[35]	0,415	[35]	–	[35]	0,423	[35]	0,306