3.1.   Плотность и термодинамика водорода, адсорбированного
на поверхности однослойных углеродных нанотрубок

Одним из интересных свойств УНТ для их практического использования является возможность адсорбирования в них различных атомов или молекул. Огромная удельная площадь поверхности ОУНТ, достигающая нескольких сотен м²/г, обеспечивает возможность адсорбирования больших количеств инертных газов, водорода, металлов, воды и т.д. Следует заметить, что сейчас признанным пределом содержания водорода в ОУНТ для его промышленного использования на транспорте считается 6 7 % (вес.) [4].

К сожалению, имеющиеся экспериментальные данные по адсорбции водорода в ОУНТ весьма противоречивы. Так, в пионерной работе Диллона (Dillon) [5] было сообщено о возможности содержания водорода в однослойных углеродных нанотрубках 5 10 % (вес.) при комнатной температуре и давлении 4 10⁴ Па. В работах [6, 7] было показано, что количество адсорбированного водорода равно 8,25 % (вес.) при 80 K и 10 MПа и 4,2 % при комнатной температуре и 10 MПа. В ОУНТ с примесью щелочных металлов по сообщению Чена (Chen) и др. [8] может содержаться от 10 до 20 % водорода. Согласно [9, 10], от 0,4 до 4 % возможно адсорбировать в ОУНТ электрохимическим путем. По данным [4], плотность адсорбированного водорода в них составляет около 3,5 %.

Существование такого большого разброса экспериментальных результатов объясняется различием применяющихся материалов и методик. При этом также отсутствует единая теория данного явления. Хотя существует достаточно работ по данной тематике [11 13], однако полного понимания сути происходящего при адсорбции водорода в нанотрубках нет.

Все применяемые методики по теоретическому описанию адсорбции водорода используют различные аппроксимации. Обычными методами здесь являются методы Монте-Карло (диффузионный (ДМК) или канонический методы), метод молекулярной динамики (МД). ДМК-метод [14] позволяет вычислять термодинамические величины, корреляционные функции и равновесную плотность частиц с учетом квантовых эффектов на основе вычисления волновой функции. Но из-за сложности реализации алгоритма температурные эффекты обычно в нем не учитываются. Канонический метод Монте-Карло [15] позволяет учитывать температурные эффекты, но использует уравнения динамики и межчастичные потенциалы взаимодействия на основе классической механики. При этом квантово-механические эффекты не учитываются. К тому же любые вычисления методом Монте-Карло требуют вычисления большого ( 10⁶) количества конфигураций, что сильно затрудняет расчеты.

Метод молекулярной динамики (как ab initio, так и на основе эмпирических потенциалов взаимодействия частиц) позволяет вычислять динамику атомов через вычисление сил, действующих на атомы. При этом атомы трактуются не квантово, а классически, подчиняющимися ньютоновским уравнениям движения. Нулевые колебания атомов, квантование уровней энергии и эффект туннелирования в данном методе не учитываются, поэтому любые МД-расчеты не могут правильно предсказать даже качественные результаты для движения частицы при низкой температуре, когда кинетическая энергия частицы меньше высоты потенциальных барьеров E_kin < E_b (необходимо все же отметить, что существуют работы, частично включающие квантовые эффекты в МД-схему расчетов для простых систем [16]).

Нами в работе [1] был предложен новый метод расчета уравнения состояния молекул водорода, адсорбированных в ОУНТ, с учетом квантово-механических эффектов, приводящих к дискретным уровням энергии и к размазанности положения адсорбируемой частицы между соседями. Методика была применена для расчета термодинамических функций и равновесной плотности одномерной цепочки молекул водорода, адсорбированных внутри сверхузких ОУНТ вида (3, 3) и (6, 0). В методе учитывалось как взаимодействие внедренных молекул между собой, так и их взаимодействие со стенками нанотрубки. При вычислении термодинамических функций при ненулевой температуре учитывались вклад фононов и эффект перехода частицы на возбужденные уровни. В данной работе рассматривается развитие данного метода применительно к расчету адсорбции водорода в ОУНТ диаметров D = 13,56 и 27,13 Å, где движение молекул водорода уже не является строго одномерным.

3.1.1.      Построение модели

Так как имеются многочисленные экспериментальные факты того, что молекулы водорода без катализаторов адсорбируются на поверхности наноуглеродных структур без образования прочных ковалентных связей, а только благодаря наличию слабого ван-дер-ваальсова взаимодействия (см. например [11]), в предложенной работе рассматривалась только физическая адсорбция. Поэтому в качестве потенциала взаимодействия был использован потенциал Сильвера Голдмена, который хорошо описывает экспериментальные данные по взаимодействию молекул H₂, включая и слабое взаимодействие ван-дер-ваальсовой природы [17, 14]. Взаимодействие с атомами углерода описывалось с помощью аналогичного потенциала [15].

Было изучено поведение молекул водорода внутри широких ОУНТ (10, 10) и (20, 20) с диаметрами   13,56  Å и 27,12 Å соответственно. При этом движение молекул водорода уже не являлось одномерным: молекулы могли смещаться от оси нанотрубки и располагаться на некотором расстоянии от стенок ОУНТ, определяемом радиусами Ван-дер-Ваальса.

Основой данной модели является решение уравнения Шредингера для волновой функции , описывающей движение частицы, рассматриваемой как целое (молекулы водорода) и находящейся в суммарном потенциале, состоящем из потенциала , создаваемого действием атомов углерода стенки нанотрубки на молекулу водорода, и из потенциала , действующего на молекулу H₂ из-за взаимодействия с соседними молекулами водорода:

(3.1)

Здесь ε_i    энергия молекулы водорода в i-м состоянии, m   масса молекулы H₂.

Было сделано предположение, что молекулы водорода должны образовывать регулярную решетку, которая может искажаться благодаря тепловым смещениям молекул (учитываемым впоследствии с помощью вклада фононов). Из-за соразмерности решеток молекул водорода и атомов углерода, выстилающих поверхность нанотрубки, следует, что решетка молекул Н₂ также должна быть гексагональной, наложенной на поверхность нанотрубки.

В расчете вероятность распределения положения частицы при каждой температуре определялась, исходя из величины , усредненной по распределению Гиббса. При этом для расчета потенциала, действующего на молекулу водорода со стороны соседних молекул, предполагалось, что позиции всех соседей являются фиксированными, определяемыми максимумом вероятности их геометрического распределения (приближение среднего поля).

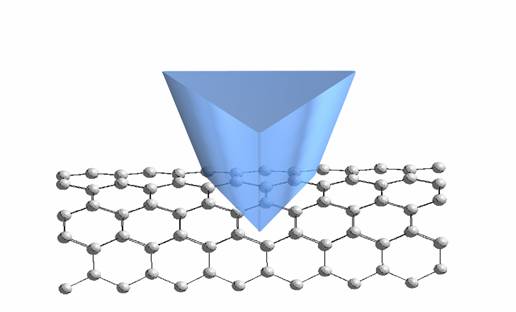
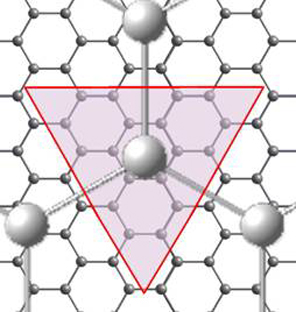
Из-за близости системы к цилиндрической симметрии и наличия графитоподобной решетки молекул водорода (а также атомов углерода) элементарная ячейка для движения молекулы водорода выбиралась в виде сужающейся треугольной призмы, ограничивающей движение молекулы областью, проекция которой на поверхность ОУНТ показана на рис. 3-1. Верхнее основание треугольной призмы выбиралось на расстоянии 1,5 Å от поверхности ОУНТ, а положение дна призмы выбиралось непосредственно вблизи оси трубки (R = 0,1 Å). Из-за резкого возрастания отталкивания при сближении молекул водорода (ближе ван-дер-ваальсова диаметра молекулы) в качестве граничных условий предполагалось, что вероятность выхода молекулы водорода за пределы призмы равна нулю. Далее путем дробления ячейки в цилиндрических координатах численно решалось уравнение Шредингера с потенциалом, действующим на частицу со стороны ее соседей и атомов нанотрубки.

Рис. 3-1. Элементарная ячейка для движений молекулы Н₂ (а), а также ее проекция (б)
на поверхность ОУНТ. Молекулы H₂   шары наибольшего размера.

При рассмотрении свойств системы при T ≠ 0 благодаря тому, что частица может переходить на возбужденные уровни энергии ε_i, средняя энергия частицы рассчитывались из распределения Гиббса:

,

(3.2)

где Z   статистическая сумма, а k_B   постоянная Больцмана.

В качестве основной исследовалась зависимость плотности адсорбированных частиц, а также равновесного расстояния между ними от внешних параметров   давления P и температуры T. Так как при внешних параметрах   равновесие системы определяется условием минимума термодинамического потенциала Гиббса   (здесь G    свободная энергия, S   энтропия, P   внешнее давление, V   объем системы), для его вычисления необходимо учитывать, кроме внутренней энергии , еще вклады энтропии S и объемной энергии PV. В свободной энергии G (в расчете на одну молекулу адсорбата) учитывались два вклада   свободная энергия G₁, связанная со средней энергией частиц   (определяемой при фиксированных положениях соседних молекул адсорбата) и энтропией S₁ их распределения по энергетическим уровням, а также фононный вклад в свободную энергию G_phon, связанный с отклонением положений этих соседей от равновесия. Такое отклонение соседних молекул от равновесия вызывает изменение уровней энергии рассматриваемой молекулы и, соответственно, изменение полной энергии системы. Это изменение энергии при смещении соседей приводит к появлению возвращающей силы, действующей на них, и к появлению вклада G_phon в свободную энергию, связанного с фононными колебаниями адсорбированных молекул, колеблющихся с частотами ω_ij:

;	(3.3)
;	(3.4)
.	(3.5)

Частоты фононов вычислялись из дисперсионного уравнения для фононов в гексагональной структуре частиц массой M, находящихся на взаимном расстоянии d и взаимодействующих с ближайшими соседями посредством упругих сил с константами f(d, T):

(3.6)

Здесь волновые векторы q_x, q_y изменяются в пределах первой зоны Бриллюэна гексагональной ячейки. Силовые константы f и, следовательно, частоты фононов рассчитывались из второй производной полной энергии системы при изменении расстояний d между молекулами H₂.

Далее вычисляя величину свободной энергии G при каждом значении (d, T) и используя формулу для давления , можно было определить Р для каждого d и, путем инвертирования, вычислить G(P, T) и Ф(P, T).

3.1.2.      Результаты и их обсуждение

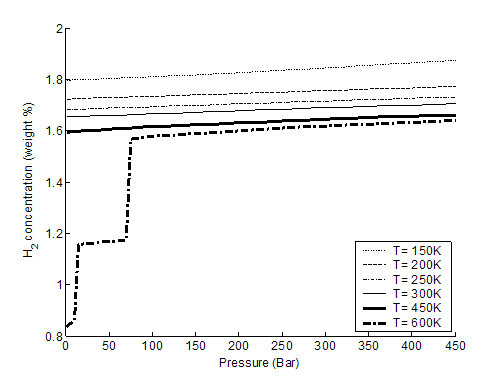
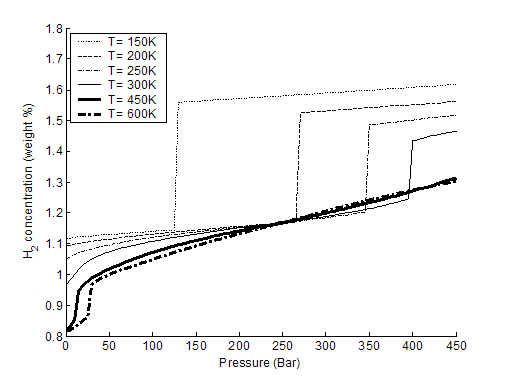
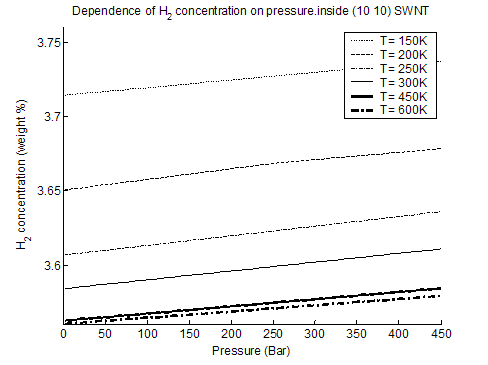
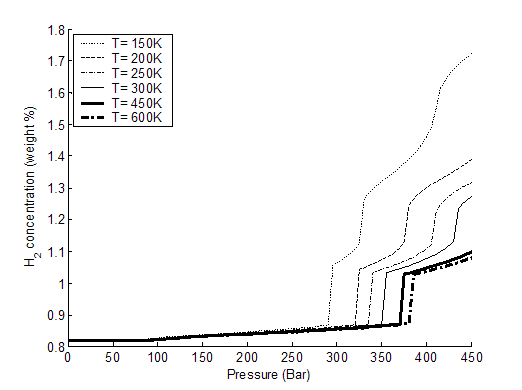
Вычисляя внутреннюю и свободную энергию частиц, а также термодинамический потенциал Гиббса Ф = Ф(Р, Т) при различных температурах и средних межмолекулярных расстояниях d, из условия минимума Ф(Р, Т) при каждом внешнем давлении Р рассчитывалась плотность m(P, T) (в весовых процентах) содержания водорода в исследуемых нанотрубках (рис. 3-2, 3-3).

Рис. 3-2. содержание Н₂ внутри ОУНТ (10, 10), %.

Рис. 3-3. содержание Н₂ внутри ОУНТ (20, 20), %.

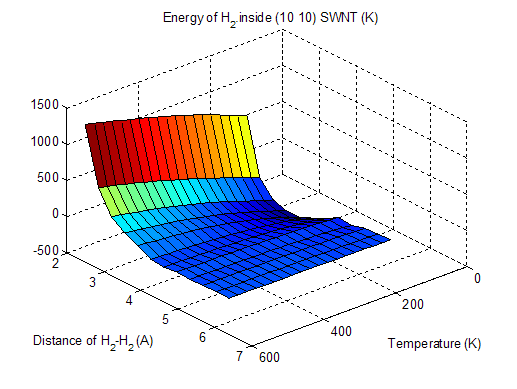
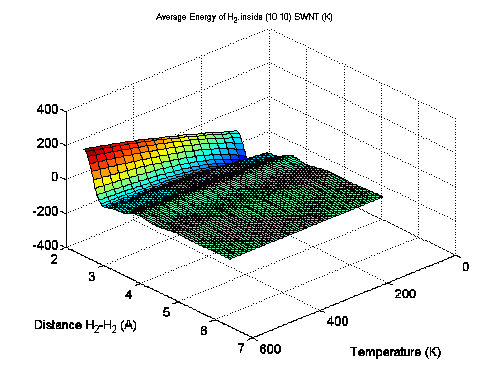
Видно, что при увеличении внешнего давления и при различных исследованных температурах плотность адсорбированных молекул водорода испытывает серию фазовых переходов. Этот эффект объясняется проявлением квантовых свойств у адсорбированных молекул водорода из-за наличия у них набора квантованных уровней энергии, заселяющихся при ненулевой температуре. На рис. 3-4 показана зависимость средней энергии молекулы водорода внутри нанотрубки (10, 10) от температуры и давления (P, T). На рис. 3-5 показана аналогичная зависимость свободной энергии молекулы водорода там же. Из рис. 3-5 видно, что свободная энергия молекулы H₂ изменяется с изменением расстояния между молекулами H₂ и температуры нелинейно, приводя в конечном итоге к фазовому переходу для плотности адсорбированного водорода при изменении давления или температуры. Косвенно на возможность такого явления указывают экспериментальные данные из работы [4].

Рис. 3-4. Средняя энергия H₂ внутри ОУНТ (10, 10).

Рис. 3-5. Свободная энергия H₂ внутри ОУНТ (10, 10).

Для доказательства наличия квантовых свойств у адсорбированных молекул водорода была рассчитана зависимость Е_тот(Р, Т) и m(P, T) для адсорбции молекул водорода с искусственно увеличенной (в 100 раз) массой внутри ОУНТ (10, 10). Эта зависимость показана на рис. 3-6.

Для оценки влияния массы на адсорбцию была использована формула аррениусовского типа для зависимости частоты десорбции частицы с поверхности [18]:

,

(3.7)

где    частота десорбции с поверхности,    частота поверхностных нормальных колебаний частицы,    энергия связи частицы с поверхностью. Полагая, что величина адсорбции m(P, T) ~ , можно установить, что величина адсорбции частиц с   должна вырасти в 10 раз (из-за корневой зависимости   от m). Из сравнения рис.  3-2 и 3-6 видно, что увеличение массы молекулы не приводит к 10-кратному увеличению m(P, T) что указывает на необходимость учета квантовых свойств для легких адсорбированных молекул.

Рис. 3-6. содержание Н₂ внутри ОУНТ (10, 10) с массой = 200 а.е., %

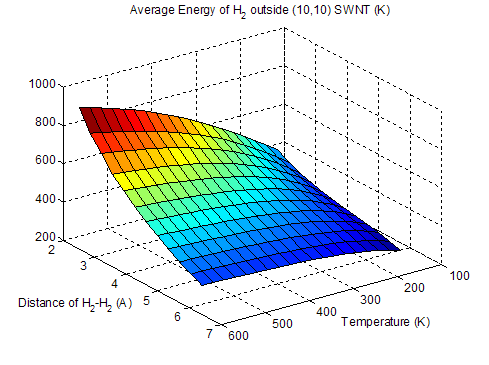
Рис. 3-7. Средняя энергия H₂ снаружи ОУНТ (10, 10).

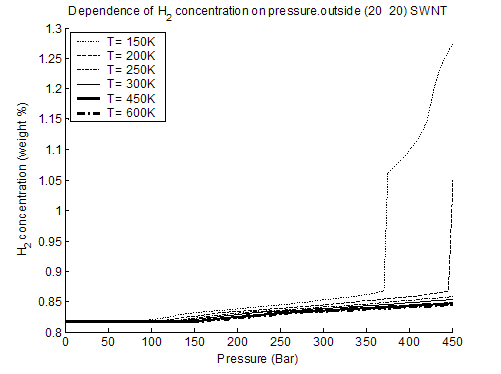
Кроме расчетов физической адсорбции водорода внутри ОУНТ были проведены такие же расчеты для адсорбции на наружной поверхности исследованных трубок (рис. 3-7 3-9). Как видно из рис. 3-8 и 3-9, давление фазового перехода увеличивается линейно с температурой для обеих исследованных нанотрубок. При этом величина адсорбции изнутри нанотрубок больше, чем снаружи. Также из сравнения данных на рис. 3-2, 3-3, 3-6 и 3-8 следует, что величина адсорбции (как изнутри, так и снаружи) уменьшается с увеличением диаметра ОУНТ. Данные зависимости связываются c увеличением эффективного ван-дер-ваальсова потенциала притяжения для молекулы водорода при увеличении кривизны нанотрубки (изнутри) и с его уменьшением снаружи.

Рис. 3-8. содержание Н₂ снаружи ОУНТ (10, 10), %.

Рис. 3-9. содержание Н₂ снаружи ОУНТ (20, 20), %

3.1.3.      Выводы к параграфу

Был предложен метод расчета термодинамических функций и равновесной плотности молекул водорода, адсорбированных внутри и вне однослойных углеродных нанотрубок различного диаметра. В методе учитываются как взаимодействия внедренных молекул между собой (в рамках приближения среднего поля), так и их взаимодействие со стенками нанотрубки. Все взаимодействия учитываются с помощью потенциала Сильвера Голдмена, включающего в себя слабое ван-дер-ваальсово межмолекулярное взаимодействие.

Модель корректно учитывает квантово-механические эффекты, приводящие к дискретным уровням энергии частицы и к эффектам переходов частицы на возбужденные уровни. При вычислении свободной энергии при ненулевой температуре учитывается вклад фононов. Данный вклад позволяет улучшить приближение среднего поля и частично учесть вклад колебаний соседних частиц относительно их средних значений в гармоническом приближении. При применении метода для расчета адсорбции молекул водорода внутри и вне ОУНТ вида (10, 10) и (20, 20) показано, что при изменении давления и температуры наблюдается последовательность фазовых переходов первого рода, приводящая к скачкообразному изменению плотности адсорбированного водорода при адсорбции как снаружи, так и внутри трубки. Установлено, что адсорбция изнутри нанотрубок больше, чем снаружи, причем ее величина (как изнутри, так и снаружи) уменьшается с увеличением диаметра ОУНТ. При этом максимальная величина адсорбции на обеих сторонах нанотрубок с диаметром ~14 Å может достигать 3,5 % (вес.) при давлении до 500 бар и T = 150 K.