1.4.2. Метод прямого вычисления одночастичной матрицы плотности
Данный вариационный
метод (см. [117]) базируется на том, что матрица плотности
является хорошо локализованной функций,
т. е. она быстро затухает при увеличении
.
Этот факт позволяет добиться общей скалируемости алгоритма как О(N). В методе
вводится единственная аппроксимация
параметр
обрезания rC, используемый для того,
чтобы ограничить недиагональные элементы матрицы плотности величинами
.
При этом метод становится точным, когда
.
В данном методе решение вариационной проблемы включает только процедуру безусловной минимизации, что может проводиться хорошо разработанным методом сопряженных градиентов и т. д. При этом метод хорошо подходит для объединения в итеративные схемы молекулярно-динамических расчетов.
Рассмотрим данный метод при применении его для описания системы, включающей N атомов с М базисными орбиталями, и с использованием метода сильной связи. Матрица плотности определяется как
|
(1.224) |
где
индексы i, j пробегают по всем базисным функциям системы, а n
по
заполненным состояниям гамильтониана. Уравнение Шредингера при этом выглядит следующим
образом:
|
(1.225) |
Стандартное решение
данного уравнения проводится с помощью разбиения объема системы на плотную
систему точек и решения полученного матричного численного уравнения для
собственных волновых функций. Альтернативно вместо этого можно попытаться
решить уравнение непосредственно для
.
В обоих случаях общее число электронов в системе и ее электронная энергия
выражаются как
|
|
|
Из условия того,
что матрица
является проекционным оператором, она должна
удовлетворять условию идемпотентности
.
Так же как и в
предыдущем методе, для минимизации полной энергии в (1.227) необходимо проводить минимизацию
при выполнении уравнения (1.226). Вместо выполнения этого условия более удобно
минимизировать канонический потенциал
при фиксированном химическом потенциале (ферми-уровне)
μ, выбираемом так, чтобы выполнялось уравнение (1.226). Без выполнения этого условия собственные состояния λр матрицы плотности будут стремиться или к
при λ р > μ (для незанятых
состояний) или к +
при λ р < μ (для
занятых состояний). Ключевым в данном методе является трюк для выполнения
условия
.
Для этого используется процедура трансформации очистки (purification
transformation), предложенная в [118]. Пусть ρ
приближенная
матрица плотности, которая почти идемпотентна. Определим очищенную матрицу,
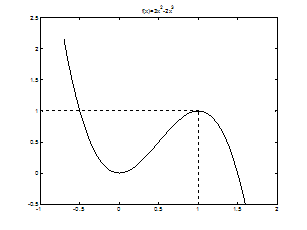
которая более близка к условию идемпотентности (рис. 1-18):
|
(1.228) |
Рис. 1-18. Функция f(x)=3x2
2x3.
Из вида этой
функции следует, что она имеет две стационарные точки
и
,
где
.
Если все собственные значения матрицы плотности попадут в эти точки, то матрица
будет идемпотентной. Если какое-то собственное значение λр>1, то
на следующей процедуре очистки это собственное значение будет возвращаться к
значению +1. Если же какое-то собственное значение λр<0, то на
следующей процедуре очистки это собственное значение будет возвращаться к
значению 0. Таким образом, с проведением процедуры очистки много раз, матрица
плотности будет все более и более приближаться к условию идемпотентности, а ее собственные
значения
к
интервалу
.
Для минимизации по
отношению к элементам
полной энергии теперь вместо минимизации (1.227) проводится минимизация следующего выражения:
|
(1.229) |
При
этом полагается, что
при
.
Здесь уже явно
никакие ограничения на систему не накладываются. При минимизации канонического
потенциала Ω ищется его локальный минимум, при котором собственные значения ρ,
соответствующие занятым и свободным состояниям, кластеризуются вокруг 1 и 0
соответственно. Минимизация обычно начинается со стартовой точки
.
Затем в процессе итеративных вычислений вычисляется градиент
|
(1.230) |
Градиент вычисляется методом наискорейшего спуска, сопряженных градиентов или другими методами. Метод позволяет также вычислять обобщенные силы, т. е. производные Ω по отношению к какому-либо параметру λ (например, к атомным координатам):
|
(1.231) |
Но первый член исчезает из-за вариационного решения, поэтому обобщенная сила вычисляется как
|
(1.232) |
В заключение можно сказать, что в данном методе:
1. Ищется
не глобальный, а локальный минимум Ω. Существуют нефизичные решения, при которых
для состояний μ и
для состояний ниже μ. К счастью, стартуя со
значений
,
метод обычно сходится к требуемым значениям
.
2. Решение для энергии представляет собой верхнюю границу точной энергии
3. Метод
становится точным, т. е.
при
.
4. Из свойств вариационных решений ошибки первого порядка в ρ приводят к ошибкам второго порядка в Ω.
5. Метод наиболее быстро сходится для изоляторов, так как в них недиагональные элементы матрицы плотности затухают более быстро.
6. Метод не требует дополнительного интегрирования по энергии в отличие от рекурсивных методов (основанных на функции Грина).
7. Наиболее
вычислительно требовательная часть алгоритма
это
перемножение ленточных матриц, т. е. получение ρ2 из ρ. Однако если
данная матрица является разреженной, к ней может быть применена эффективная техника
диагонализации, позволяющая работать с подобными матрицами достаточно больших
размеров. Разреженность матрицы гамильтониана связана, в свою очередь, с
понятием «близорукости» и локализованности волновых функций.