Глава I.4.
Решение уравнения Шредингера для движения электрона в
кулоновском поле ядра (водородоподобный атом)
Рассмотрим теперь задачу о движении электрона в
кулоновском поле ядра, т.е. задачу об атоме водорода или водородоподобном ионе.
Оператор Гамильтона такой системы будет состоять из операторов кинетической
энергии электрона и взаимодействия электрона с ядром.
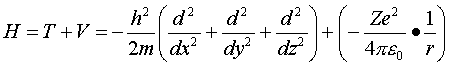 (IV.1)
(IV.1)
Однако
прежде чем записать уравнение Шредингера и приступить к его решению, условимся о
двух важных соглашениях. Во-первых, в дальнейшем, чтобы избавится от
перечисления в гамильтониане разнообразных констант, мы перейдем из системы
единиц СИ в атомную систему единиц, в которой
n
момент: h - постоянная Планка = 1
n
масса: me
- масса электрона = 1 (IV.2)
n
заряд: e - заряд электрона = 1
n
длинна: a0 - атомный радиус Бора =1
Поскольку
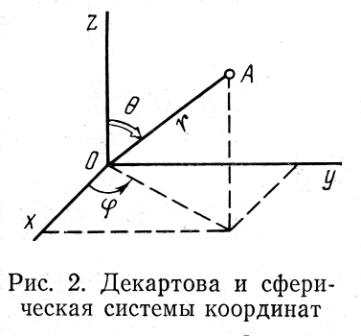
задача о движении электрона в кулоновском поле ядра обладает сферической симметрией,
то ее более естественно решать в сферических координатах ![]() , совершив переход от декартовых согласно соотношениям:
, совершив переход от декартовых согласно соотношениям:
n
![]()
n
![]()
n
![]()
n
![]()
Пределы
изменения сферических координат следующие:
|
|
Связь декартовой системы
координат со сферической системой координат. |
Оператор
Лапласа ![]() можно преобразовать к
сферической системе координат, он будет иметь вид:
можно преобразовать к
сферической системе координат, он будет иметь вид:
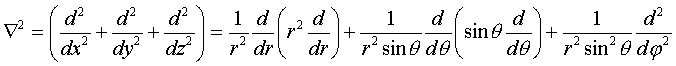 (IV.3)
(IV.3)
С
учетом всего вышеизложенного мы для атома водорода можем записать теперь
уравнение Шредингера:
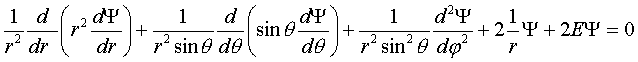
![]() (IV.4)
(IV.4)
которое
представляет собой дифференциальное уравнение второго порядка в частных
производных. Уравнения такого типа решают обычно путем разделения переменных,
т.е. волновую функцию ![]() ищут в виде:
ищут в виде:
![]() , (IV.5)
, (IV.5)
где
каждый из сомножителей зависит лишь от одной переменной. Подставим (IV.5)
в (IV.4):
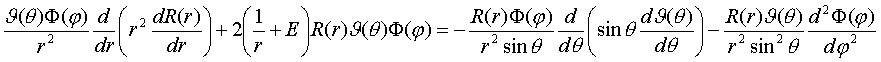 (IV.6)
(IV.6)
Помножим
обе части этого уравнения на 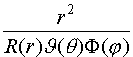 , тогда получим
, тогда получим
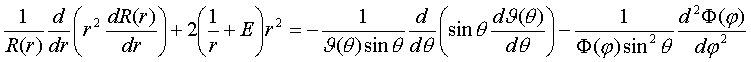 (IV.7)
(IV.7)
Легко
убедится, что левая часть равенства (IV.7) зависит только от переменной r, а правая - от переменных ![]() и
и ![]() . Но части равенства, зависящие от разных переменных, будут, в
общем случае, равны друг другу тогда и только тогда, когда левая и правая части
равны некоторой константе. Поэтому из (IV.7)
сразу же следует равенство для R(r):
. Но части равенства, зависящие от разных переменных, будут, в
общем случае, равны друг другу тогда и только тогда, когда левая и правая части
равны некоторой константе. Поэтому из (IV.7)
сразу же следует равенство для R(r):
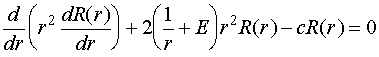 (IV.8)
(IV.8)
где
с - константа. Для правой части (IV.7) мы получим
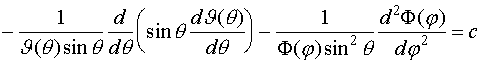
или
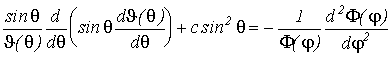 (IV.9)
(IV.9)
И
в этом равенстве левая и правая части зависят от разных переменных ![]() и
и ![]() , а поэтому они должны быть равны константе. Положим, что эта
константа положительна и равна m2,
тогда из (IV.9) следует:
, а поэтому они должны быть равны константе. Положим, что эта
константа положительна и равна m2,
тогда из (IV.9) следует:
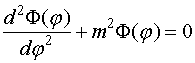 (IV.10)
(IV.10)
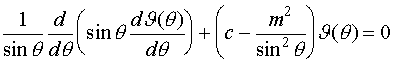 (IV.11)
(IV.11)
Тем
самым мы исходное уравнение Шредингера (IV.4), зависящее от трех переменных, свели к трем
уравнениям (IV.8), (IV.10), (IV.11),
каждое из которых зависит лишь от одной переменной. Рассмотрим теперь
эти уравнения в отдельности.
Самым
простым является уравнение (IV.10), для которого решение очевидно:
![]() (IV.12)
(IV.12)
где
А - некая константа. Условие
однозначности волновой функции дает
![]() или
или ![]() (IV.13)
(IV.13)
Воспользуемся
теперь формулой Эйлера для комплексных чисел, тогда ![]() , а это равенство выполняется лишь для целочисленных m: m=0,
, а это равенство выполняется лишь для целочисленных m: m=0,
![]()
Константу
А можно определить из условия
нормировки:
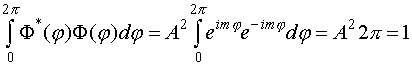
или
![]() .
.
И
тогда окончательно функция ![]() примет вид:
примет вид:
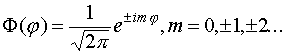 (IV.14)
(IV.14)
Рассмотрим
теперь уравнение (IV.11). Оно является
хорошо известным в теории дифференциальных уравнений уравнением Лежандра, и
тоже допускает точное решение. Это уравнение обычно решают путем замены
переменных: введем вместо ![]() новую переменную
новую переменную
![]()
![]()
![]() (IV.15)
(IV.15)
и
будем рассматривать ![]() как функцию
как функцию ![]() . Тогда (IV.11)
можно записать в виде
. Тогда (IV.11)
можно записать в виде
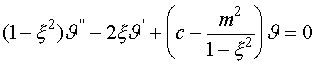 (IV.16)
(IV.16)
Рассмотрим
поведение функции ![]() вблизи особых точек
вблизи особых точек ![]() . Обратимся сначала к точке
. Обратимся сначала к точке ![]() и введем переменную
и введем переменную ![]() . Тогда из (IV.16) получим
. Тогда из (IV.16) получим
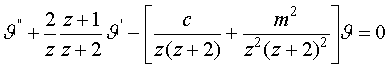 (IV.17)
(IV.17)
и
будем искать функцию ![]() в виде ряда по
степеням z:
в виде ряда по
степеням z:
![]()
![]() (IV.18)
(IV.18)
Определим
исходную степень ![]() . При
. При ![]() из (IV.18) следует:
из (IV.18) следует:
![]() (IV.19)
(IV.19)
Подставляя
это решение в (IV.17) и пренебрегая бесконечно малыми, порядка
меньше чем ![]() , мы получим:
, мы получим:
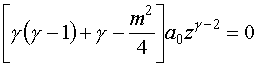 (IV.20)
(IV.20)
откуда
следует ![]() . То же значение показателя
. То же значение показателя ![]() и для особой точки
и для особой точки ![]() . Поэтому чтобы функция
. Поэтому чтобы функция ![]() была ограниченной,
необходимо, чтобы,
была ограниченной,
необходимо, чтобы, 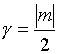 , т.е. для
, т.е. для ![]()
![]() , а для
, а для
![]()
![]() .
.
Итак,
функция ![]() тогда будет иметь
вид
тогда будет иметь
вид
![]() , где
, где ![]() - ряд по степеням z (IV.21)
- ряд по степеням z (IV.21)
Однако
для дальнейших преобразований нам удобнее представить ![]() в виде ряда по
степеням
в виде ряда по
степеням ![]() :
: ![]() . Теперь, подставив (IV.21) в (IV.16), получим
. Теперь, подставив (IV.21) в (IV.16), получим
![]() (IV.22)
(IV.22)
Если
теперь в этом выражении ![]() представить в виде
ряда по
представить в виде
ряда по ![]() и приравнять
коэффициенты при одинаковых степенях
и приравнять
коэффициенты при одинаковых степенях ![]() , то можно получить рекуррентную формулу для расчетов
коэффициентов
, то можно получить рекуррентную формулу для расчетов
коэффициентов ![]() :
:
![]() (IV.23)
(IV.23)
Если
ряд по ![]() оборвать на степени
оборвать на степени ![]() , то
, то ![]() будет многочленом k-той степени и будет решением
уравнения (IV.11). Из (IV.23) следует, что ряд может оборваться лишь в том
случае, если
будет многочленом k-той степени и будет решением
уравнения (IV.11). Из (IV.23) следует, что ряд может оборваться лишь в том
случае, если
![]() или
или
![]() (IV.24)
(IV.24)
Вводя
обозначение ![]() , мы получаем, что решение возможно лишь в случае
, мы получаем, что решение возможно лишь в случае
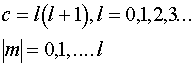 (IV.25)
(IV.25)
Итак,
решения уравнения (IV.11) зависят от характеристических чисел l и m
(легко увидеть, что эти числа есть ни что иное, как орбитальное и магнитное
квантовые числа электрона в атоме) и они имеют вид:
![]() (IV.26)
(IV.26)
где
![]() - так называемые
полиномы Лежандра, определяемые соотношением
- так называемые
полиномы Лежандра, определяемые соотношением
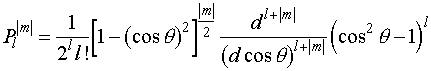 (IV.27)
(IV.27)
Для
низших значений l функции ![]() имеют вид
имеют вид
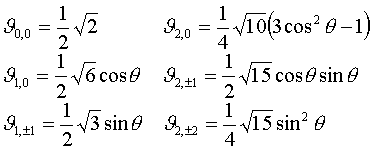 (IV.28)
(IV.28)
Итак,
мы нашли решение уравнений, зависящих от ![]() и
и ![]() . Произведение этих двух функций представляет собой угловую
часть волновой функции и называется сферической гармоникой:
. Произведение этих двух функций представляет собой угловую
часть волновой функции и называется сферической гармоникой:
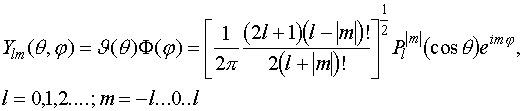
Будем
теперь решать уравнение (IV.8), зависящее от координаты ![]() .
.
Если
в это уравнение подставить уже найденное ранее значение константы ![]() (IV.25),
продифференцировать его в явном виде первое слагаемое и затем результат
разделить на
(IV.25),
продифференцировать его в явном виде первое слагаемое и затем результат
разделить на ![]() , то мы получим равенство
, то мы получим равенство
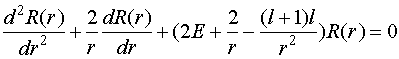 (IV.29)
(IV.29)
Решение
этого уравнения также следует искать в виде ряда по степеням ![]() :
:
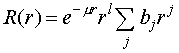 (IV.30)
(IV.30)
Здесь
![]() и
и ![]() - численные
коэффициенты.
- численные
коэффициенты.
Подставим
теперь (IV.30) в (IV.29):
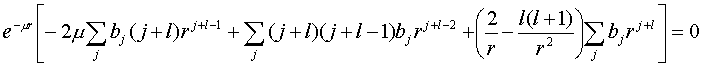 (IV.31)
(IV.31)
Очевидно,
что данное уравнение справедливо лишь в том случае, только если выражение в
квадратных скобках равно нулю при любых ![]() , а это в свою очередь выполняется ли тогда, когда равны нулю
суммы коэффициентов при одинаковых степенях
, а это в свою очередь выполняется ли тогда, когда равны нулю
суммы коэффициентов при одинаковых степенях ![]() . Отсюда следует рекуррентное соотношение для коэффициентов
. Отсюда следует рекуррентное соотношение для коэффициентов ![]() :
:
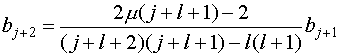 (IV.32)
(IV.32)
Функция
![]() в силу свойств
волновой функции должна быть конечной при любых
в силу свойств
волновой функции должна быть конечной при любых ![]() , т.е. ряд
, т.е. ряд ![]() должен сходиться.
Сравним этот ряд с хорошо известным разложением экспоненты
должен сходиться.
Сравним этот ряд с хорошо известным разложением экспоненты ![]() :
:
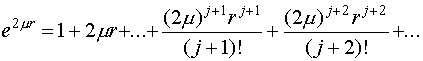 (IV.33)
(IV.33)
Отношение
двух соседних членов этого ряда равно в предположении больших ![]() :
:
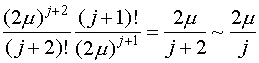
Но
отношение двух соседних коэффициентов ряда
(IV.30) при больших ![]() тоже равно:
тоже равно:
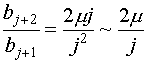 ,
,
т.е.
ряд ![]() близок к функции
близок к функции ![]() , что позволяет записать функцию (IV.30) в виде:
, что позволяет записать функцию (IV.30) в виде:
![]() (IV.34)
(IV.34)
При
![]() функция
функция ![]() вида (IV.34) стремится к бесконечности, поэтому, для
того, чтобы удовлетворить условию конечности волновой функции при любых
вида (IV.34) стремится к бесконечности, поэтому, для
того, чтобы удовлетворить условию конечности волновой функции при любых ![]() необходимо оборвать
ряд, т.е. для некоторого
необходимо оборвать
ряд, т.е. для некоторого ![]() должно выполнятся
условие
должно выполнятся
условие ![]() , или
, или
![]() (IV.35)
(IV.35)
Обозначив
![]()
мы
получим связь между ![]() и
и ![]() :
:
![]() (IV.36)
(IV.36)
Теперь,
подставив в (IV.35) значение ![]() и учитывая (IV.36), мы сразу же получим выражение для энергии
водородоподобного атома в атомных единицах:
и учитывая (IV.36), мы сразу же получим выражение для энергии
водородоподобного атома в атомных единицах:
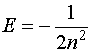 (IV.37)
(IV.37)
или
в единицах СИ
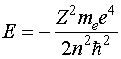 (IV.37)
(IV.37)
которое
полностью совпадает с формулой Бора.
Итак,
мы нашли решение для радиальной части волновой функции ![]() , которое с условием нормировки запишется как
, которое с условием нормировки запишется как
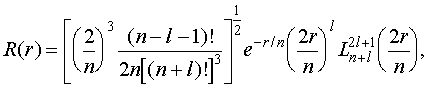 (IV.38)
(IV.38)
где
![]() - присоединенный
полином Лягера, который в явном виде равен
- присоединенный
полином Лягера, который в явном виде равен
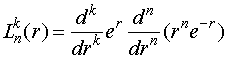 (IV.39)
(IV.39)
Для
низших значений чисел ![]() и
и ![]() присоединенные
полиномы Лягера будут иметь следующий вид:
присоединенные
полиномы Лягера будут иметь следующий вид:
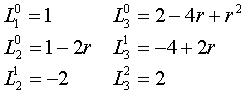 (IV.40)
(IV.40)
И
окончательно для нормированных радиальных составляющих волновой функции мы
получим:
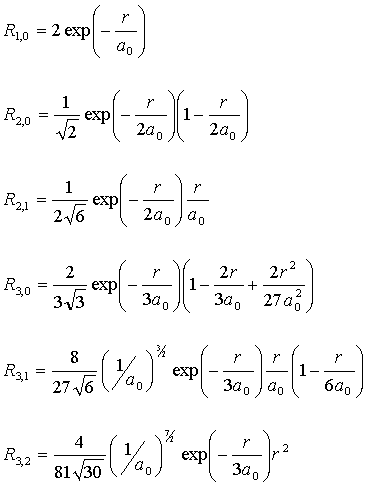 (IV.41)
(IV.41)
где
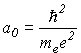
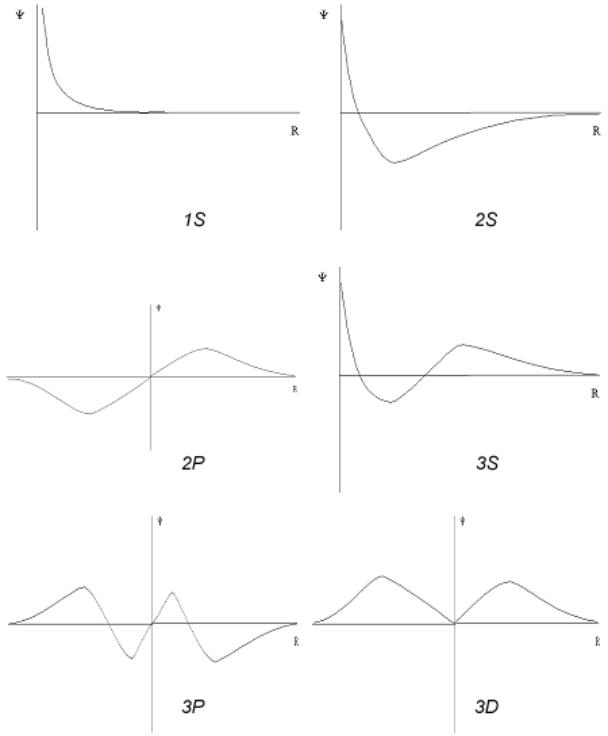
Посмотрим,
какими могут быть радиальные волновые функции: