Глава I.6.
Электронное
строение атома
Итак,
мы увидели, что решение уравнения Шредингера для атома водорода может быть
получено в виде
![]() , (VI.1)
, (VI.1)
где
каждый из сомножителей зависит или от радиус-вектора электрона, или от
координатных углов сферической системы координат, где ![]() - радиальная волновая
функция а
- радиальная волновая
функция а ![]() - угловая гармоника.
Также было показано, что волновая функция зависит от тройки целых чисел - n, l
и m , называемых квантовыми числами.
Квантовые числа могут принимать лишь строго определенные значения - 1,2,3...
Так как
- угловая гармоника.
Также было показано, что волновая функция зависит от тройки целых чисел - n, l
и m , называемых квантовыми числами.
Квантовые числа могут принимать лишь строго определенные значения - 1,2,3...
Так как
![]() (или в системе СИ
(или в системе СИ ![]() ),
),
то
n по существу определяет энергию
электрона, описываемого данной функцией, поэтому его называют главным квантовым
числом. Рассмотрим теперь второе квантовое число l. Оно вытекает из решения угловой части уравнения Шредингера,
зависит от углов ![]() и может принимать
значения l=0,1...n-1. Это квантовое
число определяет форму волновой функции. Рассмотрим теперь физический смысл
этого числа. Введем по аналогии с классическим моментом импульса
и может принимать
значения l=0,1...n-1. Это квантовое
число определяет форму волновой функции. Рассмотрим теперь физический смысл
этого числа. Введем по аналогии с классическим моментом импульса ![]() оператор момента
импульса (необходимо напомнить, что
оператор момента
импульса (необходимо напомнить, что ![]() , его направление перпендикулярно к обоим векторам
, его направление перпендикулярно к обоим векторам ![]() и
и ![]() и совпадает с направлением
поступательного движения правого винта при его повороте от
и совпадает с направлением
поступательного движения правого винта при его повороте от ![]() к
к ![]() на угол, меньший
на угол, меньший ![]() ):
):
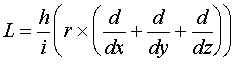 (VI.2)
(VI.2)
Вспомним,
что операторы проекций на оси координат будут:
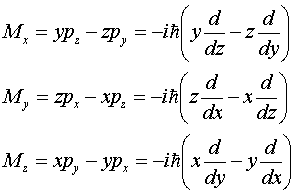
Можно
показать, что оператор квадрата момента импульса в сферических координатах
будет иметь вид
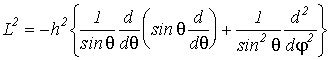 (VI.3)
(VI.3)
т.е.
с точностью до числового множителя совпадает с угловой частью оператора Лапласа
![]() , входящего в гамильтониан. Это означает, что собственные
функции оператора Гамильтона будут и собственными функциями оператора квадрата
момента импульса
, входящего в гамильтониан. Это означает, что собственные
функции оператора Гамильтона будут и собственными функциями оператора квадрата
момента импульса
![]() (VI.4)
(VI.4)
т.е.
число l определяет величину момента импульса
электрона и поэтому оно называется орбитальным.
Квантовое
число m появляется также при решении
угловой части уравнения Шредингера и может принимать значения от -l...0...l и определяет форму и
ориентацию функции в пространстве. Можно также показать, что m есть собственное значение оператора
проекции момента импульса
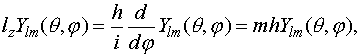 (VI.5)
(VI.5)
поэтому
его часто называют магнитным или азимутальным.
Волновую
функцию вида (VI.1) с определенными
значениями всех квантовых чисел обычно называют орбиталью (или атомной
орбиталью). Приведем явный вид некоторых орбиталей:
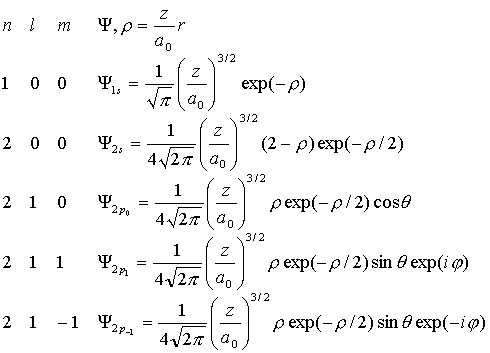 (VI.6)
(VI.6)
Как
видно из таблицы, орбитали с l=0 не
зависят от угловых координат, т.е. имеют сферическую форму. Орбитали с l=1
имеют сложную форму с исторически сложившимся названием - гантели,
причем с различными знаками волновой функции по разные стороны начала
координат. Необходимо отметить, что p-
орбитали с l=1 и l=-1 - комплексны, а значит
с ними работать неудобно. Однако, поскольку любые комбинации p- орбитали являются опять p- орбиталями, то
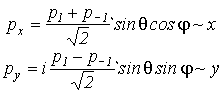 (VI.7)
(VI.7)
которые
уже соответственно ориентированы вдоль декартовых осей координат.
Рассмотрим
теперь более сложную задачу - атом гелия. Оператор Гамильтона для него будет иметь
вид:
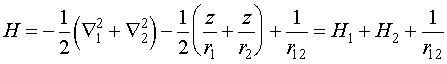 (VI.8)
(VI.8)
Точное
решение уравнения Шредингера с таким гамильтонианом неизвестно, поэтому оно
решается приближенными методами.
Необходимо
отметить, что гамильтонианы H1
и Н2 - по сути являются
гамильтонианами для атома водорода с тем отличием, что заряд ядра равен 2.
Решим теперь эту задачу с помощью теории возмущений, положив
![]() и
и 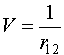 (VI.9)
(VI.9)
Известно,
что задача с нулевым гамильтонианом допускает точное решение, так как переменные
первого и второго электронов становятся независимыми. Тогда
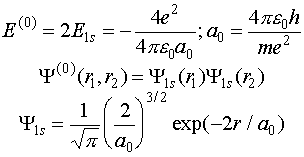 (VI.10)
(VI.10)
Теперь,
по теории возмущений учтем межэлектронное взаимодействие
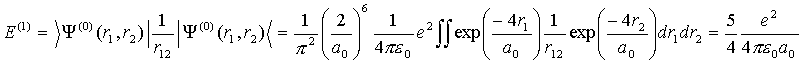 (VI.11)
(VI.11)
Тогда
полная энергия атома гелия будет равна
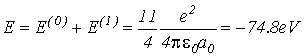 (VI.12)
(VI.12)
Ту
же задачу можно решить и вариационным методом, причем двумя способами. Атом
гелия имеет два электрона. Эффективное кулоновское поле, порождаемое этими
электронами, фактически ослабляет притяжение каждого электрона ядром, что
формально можно записать, как уменьшение эффективного заряда ядра. Это дает
возможность записать волновую функцию в виде:
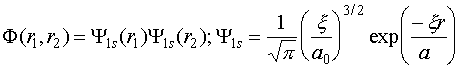 (VI.13)
(VI.13)
где
![]() - неизвестный параметр
- эффективный заряд ядра.
- неизвестный параметр
- эффективный заряд ядра.
Рассчитаем
теперь функционал энергии:
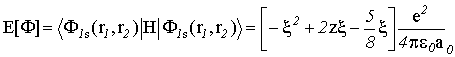 (VI.14)
(VI.14)
Продифференцировав этот интеграл по ![]() , мы, из условия
, мы, из условия ![]() , получим:
, получим:
![]() и
и ![]() . (VI.15)
. (VI.15)
Итак,
эффективный заряд ядра будет равен ![]() .
.
Можно
провести гораздо более сложный расчет с применением многоэлектронной функции
вида
![]() (VI.16)
(VI.16)
где
с - некоторые коэффициенты. В этой функции подлежат определению
коэффициенты c, и она замечательна тем,
что в ней не разделяются переменные первого и второго электронов.
Результаты
расчетов этими методами можно представить в виде таблицы:
|
Метод |
Полная энергия |
Ошибка |
Потенциал ионизации |
|
ТВ |
-74.8 эВ |
»5% |
20.4 эВ |
|
ВМI |
-77.45 эВ |
»2% |
23.05 эВ |
|
ВМII |
-78.98 эВ |
»0/1% |
24.35 эВ |
|
эксперимент |
-79.02 эВ |
- |
24.58 эВ |
Выше
мы рассмотрели строение волновой функции атома гелия, точнее, той ее части,
которая зависит от пространственных координат электронов. Однако как уже
говорилось ранее, электрон наряду с пространственным положением характеризуется
еще дополнительной величиной - собственным моментом количества движения или
спином, поэтому естественно предположить, что полная волновая функция любой
многоэлектронной системы будет зависеть как от пространственных, так и от
спиновых переменных. Причем спиновые переменные могут принимать только два
значения: ![]() . Часть волновой функции, зависящая от спина (спин-функция)
должна удовлетворять уравнениям на собственные значения
. Часть волновой функции, зависящая от спина (спин-функция)
должна удовлетворять уравнениям на собственные значения
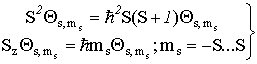 (VI.17)
(VI.17)
операторов
квадрата спина и его проекции на ось z.
Для
системы из двух электронов суммарный спин может принимать два значения: S=0 (и
тогда ms=0) и S=1 (и тогда ms=-1, 0 +1), т.е. согласно (VI.17) мы можем записать четыре
спин-функции
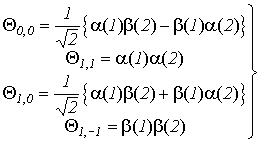 (VI.18)
(VI.18)
Далее,
поскольку в оператор Гамильтона (VI.8)
для атома гелия спиновые координаты в явном виде не входят, то это означает,
что полную волновую функцию можно записать как произведение пространственных и
спиновых частей:
![]() (VI.18)
(VI.18)
а
поскольку волновая функция фермионов должна быть антисимметричной:
![]() (VI.19)
(VI.19)
то
это означает, что если проекцию спина ms рассматривать как четвертое
квантовое число, то можно сформулировать так называемый принцип запрета Паули: в атоме не может быть двух электронов с одинаковым набором квантовых
чисел.
Итак,
на примере атомов водорода и гелия мы с вами увидели, что довольно часто
встречается ситуация, когда несколько волновых функций имеют одинаковую
энергию, т.е. являются вырожденными, причем это вырождение может возникать как
за счет орбитального (степень вырождения (2l+1)) момента, так и за счет
спинового (степень вырождения (2S+1)). Причем для многоэлектронного атома это
вырождение может частично сниматься за счет электронного взаимодействия. Другими
словами это означает, что в отсутствие межэлектронного взаимодействия для,
скажем, конфигурации 2p13p1 имеется девять вырожденных
по l положений электрона:
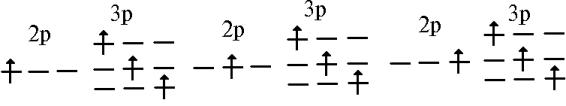
Однако
взаимное отталкивание электронов приводит к тому, что некоторые из указанных распределений
электронов (микросостояний) будут иметь более высокую энергию, а некоторые -
более низкую. Такую классификацию можно провести, основываясь на полном моменте
импульса:
![]() (VI.20)
(VI.20)
который
является суммой орбитальных и спиновых моментов всех электронов. Если считать,
что спин-орбитальное взаимодействие мало, то орбитальный и спиновый моменты
можно рассматривать по отдельности, используя для нахождения входящих в (VI.20) сумм правила сложения моментов:
если l1 и l2 - квантовые числа моментов
двух частиц, то суммарный момент может быть равен одному из следующих чисел:
![]() (VI.21)
(VI.21)
Итак,
при наличии электронного взаимодействия вырожденные водородоподобные уровни распадаются
на несколько групп, характеризующихся суммарным орбитальным и спиновым
моментами, называются термами. Для обозначения термов используют прописные
латинские буквы, совпадающие со значениями орбитального числа l, а в левом верхнем углу указывают вырождение
по спину (2S+1) или мультиплетность:
|
L |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
.... |
|
S |
0 |
1/2 |
1 |
0 |
1/2 |
1 |
3/2 |
.... |
|
терм |
1S |
2S |
3S |
1P |
2P |
3P |
4P |
.... |
Для
рассмотренной конфигурации 2p13p1 (суммарная степень вырождения
(n!(1))(n!(2))=36, где n(1) и n(2) - количество состояний 1-го и 2-го
электронов) мы получаем следующую совокупность термов:
|
L= |
2, 1, 0 |
S= |
1, 0 |
Þ |
3D; 3P; 3S |
|
количество |
состояний |
(2l+1) |
(2S+1) |
|
15 9 3 |
|
|
D P S |
M= |
3, 1 |
|
1D; 1P; 1S |
|
количество |
состояний |
(2l+1) |
(2S+1) |
|
5 3 1 |
т.е.
изначально вырожденный уровень распадается на шесть подуровней, которые также вырождены,
но их кратность вырождения существенно меньше и равна (2l+1)(2S+1)
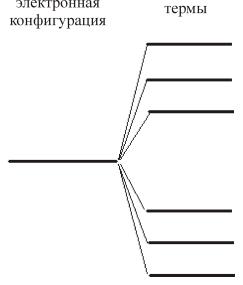
Следует
также подчеркнуть, что это расщепление относительно невелико, порядка 1 эВ,
тогда как разница между энергиями конфигураций, как правило, не менее 10 эВ.
Выше
мы рассмотрели вариант классификации термов в предположении, что
спин-орбитальное взаимодействие мало (случай L-S связи), который хорошо зарекомендовал себя для легких атомов.
Для тяжелых атомов предпочтительнее пользоваться так называемой J-J связью, когда сначала определяется
суммарный момент электрона li+Si,
а термы классифицируются по полному моменту J.
Для
определения термов группы эквивалентных электронов (n и l совпадают)
процедура несколько усложняется из-за необходимости учета принципа Паули и
обычно проводится путем непосредственного подсчета микросостояний. Рассмотрим
конфигурацию p2: возможные
значения L: 2; 1; 0, S: 0; 1, а для проекций соответственно ML: 2, 1, 0, -1, -2 и MS: 1, 0, -1. Строим таблицу
микросостояний, не противоречащих принципу Паули:
|
ML/ MS |
1 |
0 |
-1 |
|
2 |
|
(1+1-) |
|
|
1 |
(1+0+) |
(1+0-)(1-0+) |
(1-0-) |
|
0 |
(1+-1+) |
(1+-1-)(0+0-)(1—1+) |
(1--1-) |
|
-1 |
(0+-1+) |
(0+-1-)(0—1+) |
(0—1-) |
|
-2 |
|
(-1+-1-) |
|
Итого,
мы получили ![]() микросостояний.
Выделим теперь те, которые отвечают электронным термам, начиная с максимальных
значений ML и MS . ML=2, следовательно, L=2,
т.е. первый терм D-типа. Поскольку MS =0, то его мультиплетность
равна единице и, следовательно, это 1D
- терм. Кратность его вырождения равна 5. Следующий терм характеризуется ML=1 и является триплетным по
спину. Это терм 3P.
Кратность его вырождения равна девяти. Остается лишь одно состояние с ML=MS =0, это 1S
терм. Итак, для конфигурации p2
мы имеем три терма: 1D, 3P и 1S.
микросостояний.
Выделим теперь те, которые отвечают электронным термам, начиная с максимальных
значений ML и MS . ML=2, следовательно, L=2,
т.е. первый терм D-типа. Поскольку MS =0, то его мультиплетность
равна единице и, следовательно, это 1D
- терм. Кратность его вырождения равна 5. Следующий терм характеризуется ML=1 и является триплетным по
спину. Это терм 3P.
Кратность его вырождения равна девяти. Остается лишь одно состояние с ML=MS =0, это 1S
терм. Итак, для конфигурации p2
мы имеем три терма: 1D, 3P и 1S.
Относительную
энергию термов можно определить по правилу Хунда:
n
Самым низким по энергии
является терм с максимальной мультиплетностью
n
Если мультиплетность одинакова,
то низшим по энергии будет терм с максимальным значением L
Следует
отметить, что электронные конфигурации с числом электронов n и (m-n), где m- максимально возможное число электронов на подуровне, имеют
одинаковый набор термов.