1.3.2. Многочастичные потенциалы

1.3.2.1. Потенциал Стиллингера

Вебера

Потенциал Стиллингера Вебера (Stillinger Weber) [66] является одним из первых потенциалов, описывающих материалы, образующие алмазоподобную структуру (C, Si, GaAs, Ge). Потенциальная энергия этого потенциала записывается в следующем виде:

.

(1.174)

Здесь θ_ijk   угол, центрированный на атоме i, R_C   радиус обрезания потенциала.

При β = cos(109,47°) = 1/3 энергетически выгодной является алмазоподобная конфигурация. Потенциал Стиллингера Вебера является достаточно популярным и часто применяется в численных расчетах кристаллического кремния [67, 68].

Основной проблемой данного потенциала является его плохая переносимость, поскольку трехчастичный вклад в (1.174) имеет только одну равновесную конфигурацию при β =  1/3. Однако в случае углерода, кроме 109,47°, стабильными являются конфигурации с углами 180° и 120°. Также данный потенциал дает неверные результаты в случае его использования для оптимизации поверхности кристалла кремния и кремниевых кластеров малых размеров.

Этих недостатков лишен потенциал Абеля Терсоффа Бреннера, разработанный для углерода и его соединений с водородом и основанный на зависимости прочности связи от локального атомного окружения.

Таблица 1-5. Параметры потенциала Стиллингера Вебера для кремния

1.3.2.2. Потенциал Абеля

Терсоффа

Бреннера

Общая форма этого потенциала была предложена Абелем (Abel) [69], после чего он был доработан Терсоффом (Tersoff) [70] и впоследствии параметризован для углерода и его соединений с водородом Бреннером (Brenner) [71, 72]. Данный потенциал широко используется для молекулярно-динамических расчетов углеродных соединений (таких как углеродные кластеры, нанотрубки и т. п.) [73 78]. Потенциал Абеля Терсоффа Бреннера (ПАТБ) хорошо описывает механические свойства подобных структур, упругие свойства и зависимость динамики данных структур от температуры.

Потенциальная энергия, полученная с использованием ПАТБ, записывается в следующем виде:

,

(1.175)

где r_ij   расстояние между ближайшими соседними атомами i и j, b_ij   порядок связи между атомами i и j:

.

(1.176)

Значение функции зависит от атомного окружения и угла связи для атома i. Функция также состоит из двух членов:

.

(1.177)

Выражения (1.176) и (1.177), скомбинированные с (1.175), используются для определения энергии связи из-за ковалентного связывания любого набора атомов углерода и водорода.

Член, связанный с межатомным отталкиванием и притяжением (1.175), записывается в следующем виде:

,	(1.178)
.	(1.179)

Экранированная кулоновская функция используется для описания парного отталкивания в (1.178), а функция ограничивает радиус ковалентного взаимодействия. В случае описания углеродной системы предполагается, что функция равна единице для ближайших соседей и нулю в любом другом случае.

Первый член в уравнении (1.176) записывается в следующем виде:

,

(1.180)

где функция P   это бикубический полином, а числа и    это количество соседних атомов углерода и кислорода. Они определяются следующим образом:

,	(1.181)
.	(1.182)

Функция в (1.180) определяет вклад в порядок связи между атомами i и j со стороны соседнего атома k как косинус угла j i k (табл. 1-6, 1-7, рис. 1-12, 1-13). Аналитический вид функции для углерода был получен как полином шестого порядка. Вся информация для конструирования этого полинома дана в табл.  1-6.

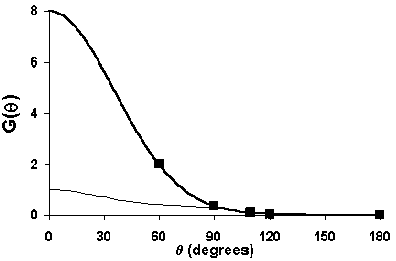
Рис. 1-12. Вид полиномов G_C(θ) (жирная линия) и γ_C(θ) (тонкая линия). Отмеченные точки
соответствуют значениям, приведенным в табл. 1-6.

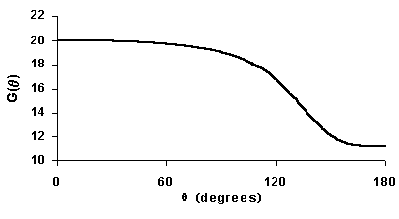
Рис. 1-13. Вид полинома G_H(θ).

Полином γ(θ) должен быть использован для систем с избыточным и недостаточным числами соседей. Таким образом, общая угловая функция для углов, больших 0, но меньших, чем 109,47°, для атома углерода i имеет следующий вид:

.

(1.183)

Общая угловая функция для атома водорода имеет вид .

Функция Q в (1.183) определяется как

(1.184)

Здесь    координационное число атома i:

.

(1.185)

Первый член в (1.177) зависит от полного числа соседей связанных атомов i и j и от функции , определяющей, является ли связь частью сопряженной системы:

,

(1.186)

где

(1.187)

и

.

(1.188)

Если все атомы углерода связаны в пары, i и j имеют четыре соседа или более, то уравнения (1.186) (1.188) определяют   равным единице. Таким образом, связь между этими атомами не является частью сопряженной системы. При уменьшении координационных чисел соседствующих атомов   становится больше единицы, показывая, что связь становится частью сопряженной системы. Например, значение N^conj для углерод-углеродной связи в графите равно девяти, в то время как для бензола N^conj = 3. Значения F даны в табл. 1-8. Интерполяцию между ними следует проводить с помощью трикубического полинома (табл. 1-9).

Последний член в (1.177) имеет следующий вид:

,

(1.189)

где

.

(1.190)

Здесь функция    трикубический полином (табл. 1-9); e_jik и e_ijl   единичные векторы, направленные параллельно векторным произведениям и   соответственно, где    вектор, соединяющий атомы i и j.

Значения функции T_C-C даны в табл. 1-10, параметры для уравнений (1.178) и (1.191)   в табл. 1-11 1-14 .

Функция, определяющая радиус ковалентного взаимодействия, имеет следующий вид:

(1.191)

где разность   определяет расстояние, на котором функция  меняется от единицы да нуля.

1.3.2.3. Потенциал Клери

Росато

Потенциал Клери Росато (Cleri Rosato) [79] может быть применен для описания переходных металлов (ГЦК и ГПУ) и сплавов (табл. 1-15, 1-16). Данный потенциал корректно описывает динамику решетки этих материалов, а также их поведение при ненулевой температуре.

Энергия связи системы записывается в следующем виде:

,

(1.192)

где r_ij   расстояние между текущим атомом i и атомом j;    расстояние до ближайшего соседа; ξ   эффективный интеграл перескока; q описывает зависимость ξ от относительного межатомного расстояния. ξ и q предполагаются зависящими только от типов взаимодействующих атомов α и β.

Суммирование по j в уравнении (1.192) идет вплоть до соседей пятого порядка в кубической структуре и до соседей девятого порядка в гексагональной плотноупакованной структуре.

Для переходных металлов, образующих гексагональную плотноупакованную структуру, необходимо ввести новый параметр (где c и a   параметры элементарной ячейки).

Кроме вышеописанного, было предложено множество других эмпирических потенциалов: для гранецентрированных металлов были разработаны потенциалы «Сандиа» («Sandia») (Au, Cu, Pd, Ag, Pt, Ni, Al, некоторые сплавы) [80 82], Джонсона (Johnson) для большинства подобных металлов [83] и их сплавов [84], «стыковочные» («glue») (Au, Al) [84 87], потенциалы Вотера Чена (Voter Chen) для Al и Ni [88], для сплава Ni₃Al [89]. Для металлов с гексагональной плотноупакованной структурой были разработаны потенциалы Оха Джонсона (Oh Johnson) (Mg, Ti, Zr) [90], Пасионато Савино (Pasionat Savino) (Hf, Ti, Mg, Co) [91]. Для ОЦК металлов были предложены следующие потенциалы: потенциал Финниса Синклера (Finnis Sinclair) (Fe, V, Nb, Ta, Mo, W) [92, 93] и Оха Джонсона (Li, Na, K, V, Nb, Ta, Cr, Mo, W, Fe) [94].