1.2.3. Метод сильной связи

Метод сильной связи (МСС) является полуэмпирическим методом расчета, основанным на замене многочастичного гамильтониана на параметризованную матрицу гамильтониана, с последующей диагонализацией последней. МСС показывает хорошие результаты при расчете систем, связанных с помощью ковалентного взаимодействия, и для переходных металлов. Также он параметризован для других химических элементов [54]. МСС может быть применен для расчета геометрической и электронной структур, а также проводимости, энергии ионизации, энергетических зон и т. д., как для периодических и аморфных твердых тел, так и для атомных кластеров [12].

1.2.3.1. Теория МСС

Пусть исследуемая волновая функция   ( j = 1, …, n), где n   число волновых функций Блоха, может быть представлена в виде линейной комбинации функций Блоха   следующим образом:

,

(1.159)

где C_jj’   неизвестные коэффициенты, которые необходимо найти. Поскольку волновая функция   должна также удовлетворять теореме Блоха, суммирование в (1.159) идет только по блоховским орбиталям   с одинаковым значением волнового вектора.

j-е собственное значение может быть получено из следующего выражения:

,

(1.160)

где H   гамильтониан исследуемой системы. Подставляя (1.159) в (1.160), можно получить следующее уравнение:

,

(1.161)

где H_jj’ и S_jj’ называются матрицами интеграла переноса и интеграла перекрытия соответственно:

.

(1.162)

Коэффициенты   определяют энергетический минимум, т.  е.

.

(1.163)

Умножив (1.163) на   и подставив выражение для   из (1.161) во второй член (1.163), можно получить следующее равенство:

.

(1.164)

Или в векторном виде:

,

(1.165)

где

.

(1.166)

Из выражения (1.165) можно получить уравнение на собственные значения:

(1.167)

из которого можно получить все n собственных значений   ( i = 1, …, n) для данного значения . Собственные значения энергии    это периодичные функции в обратном пространстве в первой зоне Бриллюэна.

1.2.3.2. Алгоритм расчета методом сильной связи

На следующей блок-схеме представлен алгоритм расчета с помощью метода сильной связи.

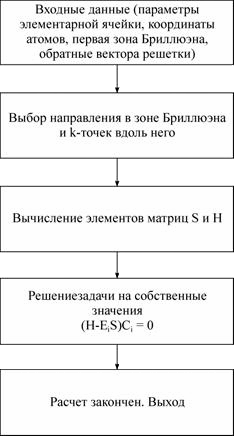
Входные данные: Определение элементарной ячейки и параметров решетки . Определить координаты атомов в ячейке и выбрать n атомных орбиталей для расчета. Определить зону Бриллюэна и обратные вектора решетки .

Выбор направления в зоне Брюллиэна и k-точек вдоль него.

Вычисление элементов матриц S и H: Для выбранных k-точек вычислить элементы матриц переноса H_ii’ и перекрытия S_ii’(1.162) [7].

Решение задачи на собственные значения: Для выбранных k-точек решается характеристическое уравнение (1.167) [55].