Глава I.5.
Основные методы приближенного уравнения
Шредингера
Ранее
мы убедились, что решение уравнения Шредингера даже для таких простых
физических систем, как атом водорода представляет собой достаточно сложную
математическую задачу. Естественно, что при увеличении числа частиц в системе
это решение еще более усложнится. В настоящее время точных решений уравнения
Шредингера для систем многих частиц, т.е. для систем более сложных, нежели чем
молекулярный ион Н2+. Именно поэтому особое значение
приобретают способы приближенного решения уравнения Шредингера, которых
известно довольно много, но которые можно разделить на две большие группы:
методы теории возмущений и вариационные методы. Ниже мы рассмотрим основные
принципы построения этих методов.
Основная
идея теории возмущений состоит в том, что все взаимодействия в системе можно
условно разделить на «основные» и «второстепенные» по каким-либо признакам,
например - энергетическим. В ряде случаев такие качественные соображения
позволяют внести в исходный оператор Гамильтона какие-либо изменения,
позволяющие свести исходную задачу к существенно более простой, допускающей
точное решение. Однако после того как было получено решение модельной задачи с
упрощенным Гамильтонианом, необходимо все-таки учесть отброшенные поправки.
Решением таким способом и занимается теория возмущений, позволяющая явным
образом описать изменение («возмущение») решений уравнения Шредингера при малом
изменении Гамильтониана. Чтобы можно было говорить о малости вносимых
изменений, введем так называемый параметр возмущения l, изменение которого описывает изменение оператора
Гамильтона. Например, молекулу водорода при больших межъядерных расстояниях
можно трактовать как взаимодействие двух атомов водорода и тогда 
и при 
и задача сводится к
двум свободным атомам водорода.
С
формальной точки зрения такой подход означает, что в исходном уравнении
Шредингера
(V.1)
исходный
Гамильтониан представляется в виде:
(V.2)
где
- гамильтониан
невозмущенной задачи, для которой известно точное решение:
(V.3)
Далее
попытаемся исследовать, что произойдет с решениями уравнения (V.3)
при возмущении гамильтониана, полагая,
что в силу малости параметра 
и собственные
функции, и собственные значения возмущенной задачи (V.1) можно представить в виде рядов:
(V.4)
(V.5)
Подставим
теперь ряд (V.4) в левую часть
уравнения (V.1):
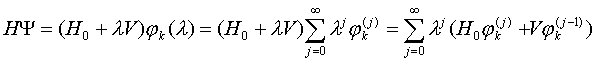(V.6)
Здесь
для объединения членов переобозначили 
, а затем опустили апостроф, так как при больших 
это выражение
выполняется. Для единообразия при 
введем член 
, который будем считать равным нулю. Подстановка рядов (V.4) и (V.5)
в правую часть равенства (V.1)
дает
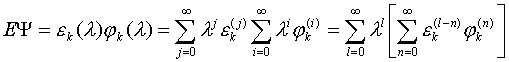(V.7)
Ну
а поскольку и (V.6) и (V.7) есть части одного равенства, то
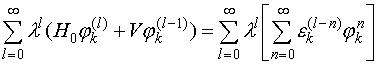(V.8)
Последнее
равенство будет справедливо лишь в том случае, когда слагаемые при одинаковых
степенях 
будут равны, т.е.
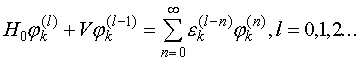(V.9)
или
в явном виде
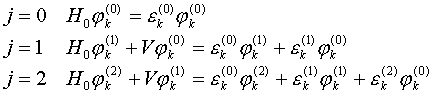(V.10)
Попытаемся
теперь получить поправки к энергии 
и к волновой функции 
в явном виде. Далее,
поскольку 
есть решение
уравнения Шредингера (V.3), то интеграл в обозначениях Дирака запишется:
(V.11)
Предположим,
что поправки к волновой функции ортогональны 
:
(V.12)
домножим
второе уравнение (V.10) слева на 
и проинтегрируем:
(V.13)
Поскольку
- собственная функция
и с учетом
условий (V.11) и (V.12)
последнее равенство сведется к виду:
(V.14)
т.е. поправка к энергии первого порядка
равна среднему значению оператора возмущения, вычисленному на собственных
функциях невозмущенной задачи.
Если
то уравнение (V.13) примет вид:
или
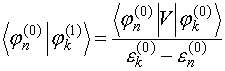(V.15)
Из
последнего равенства можно получить в явном виде выражение для поправки первого
порядка к волновой функции, для этого (V.15)
надо справа домножить на 
и проинтегрировать.
Но поскольку индекс n
не фиксирован, то
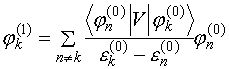(V.16)
Совершенно
аналогично из третьего уравнения (V.10)
можно получить поправки второго порядка к энергии и к волновой функции:
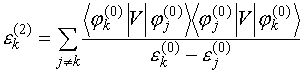(V.17)
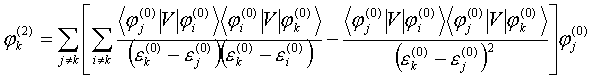(V.18)
Из
выражений (V.14) - (V.18) следует, что волновая функция, определенная
с точностью до S- го порядка, дает энергию до (2S+1)
- го порядка, т.е. энергия при использовании теории возмущений быстрее сходится
к «точному» значению, чем волновая функция.
Теория
возмущений в варианте, изложенном выше, называется теорией возмущения
Релея-Шредингера, причем она была получена в предположении, что все собственные
значения уравнения (V.3)
являются невырожденными. В случае, если невозмущенный Гамильтониан 
имеет вырожденные
собственные значения, задача построения теории возмущений несколько
усложняется, поскольку в выражениях для поправок к энергиям и собственным функциям
входят в качестве знаменателей разности энергий, а для вырожденных значений
энергии по определению равны, а значит - возникает деление на 0, и собственно
члены ряда будут обращаться в бесконечность. С другой стороны, поскольку
возмущение 
предполагается малым,
то естественно предположить, что функции, появляющиеся при возмущении из
функций вырожденного уровня будут какой-либо линейной комбинацией исходных
вырожденных функций, при этом обозначим кратность вырождения энергии 
как 
:
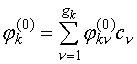(V.19)
где
- некоторый
коэффициент. Подставив теперь (V.19)
во второе уравнение (V.10)
получим:
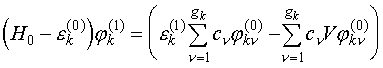(V.20)
Домножим
слева это уравнение на 
и проинтегрируем.
Тогда в силу уравнения (V.3)
левая часть полученного равенства будет равна нулю, т.е.
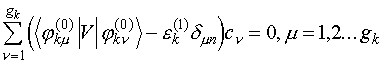(V.21)
Последнее
соотношение есть ни что иное, как система линейных алгебраических уравнений
относительно 
и она имеет ненулевые
решения лишь при условии
(V.22)
Раскрывая
этот детерминант и решая его относительно 
, мы можем определить 
его корней,
подстановка которых в уравнение (V.21)
даст нам наборы коэффициентов 
и соответственно
нулевые приближения, но уже с учетом возмущения. Поскольку теперь в задаче
вырождение снято, и каждый вырожденный уровень расщепился 
, то дальше задачу можно решать обычными методами теории
возмущений.
Вторым,
не менее мощным методом нахождения решений уравнения Шредингера является
вариационный метод, который в отличие от теории возмущений основан не на упрощении
гамильтониана, а на упрощении волновой функции. Основная идея вариационного
метода проста: с одной стороны, согласно постулатам квантовой механики полную
энергию системы мы можем рассчитать как
(V.23),
а
с другой стороны, согласно общим физическим принципам любая система стремится к
состоянию с минимальной энергией. Поэтому если мы последовательно будем
рассчитывать интегралы (V.23) с
различными пробными функциями Ф, то
тогда та функция, которая даст минимальное значение Е может в каком-то приближении считаться решением уравнения
Шредингера. Естественно, что вручную перебрать достаточно большое количество
функций невозможно, однако задачу можно оптимизировать, так как она во многом
напоминает задачу нахождения экстремума какой-либо функции. Действительно, мы
должны отыскать минимум функции от функции или функционала (V.23) относительно изменений пробных функций Ф. Введем, по аналогии с дифференциалом, понятие «вариация функции»
(или вириал), т.е. какое-либо допустимое ее изменение, для которого формально
выполняются все те правила, что и для дифференциала. Тогда задачу поиска
решений уравнения Шредингера можно сформулировать как задачу поиска
экстремальных точек функционала энергии относительно вариаций функции Ф:
(V.24),
Поскольку
исследовать все функции нельзя, то задача de facto сводится к двум проблемам:
n
Определение класса пробных
функций;
n
Поиск в указанном классе
оптимальной в смысле энергии функции.
Вариационный
метод хорош тем, что допускает систематическое уточнение, а именно: если мы
рассматриваем класс пробных функций, то минимальное значение Е может только уменьшаться, или, во
всяком случае, не возрастать. Можно доказать и более сильное утверждение: в
вариационном методе мы всегда получаем оценку энергии сверху. Действительно,
пусть известна совокупность решений 
уравнения Шредингера
(V.25)
Возьмем
теперь пробную функцию Ф и
рассчитаем функционал энергии (V.24).
Поскольку оператор Н -
самосопряженный, то его собственные функции образуют полный ортонормированный
набор, а это означает, что Ф можно
представить в виде ряда:
(V.26).
Но
тогда:
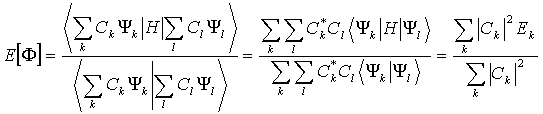(V.27).
Заменяя
в числители все 
на 
и учитывая (V.25), находим, что
(V.28),
откуда
следует:
(V.29),
т.е.
при любой пробной функции Ф мы
получаем оценку сверху для минимальной точной энергии системы. Из (V.29) также следует, что при 
, т.е. при минимизации функционала энергии пробная функция
стремится к точной волновой функции системы.
Естественно,
что с практической точки зрения уравнения (V.25)
- (V.29) мало интересны, т.к. в них фигурируют точные решения уравнения
Шредингера, которые, как правило, не известны.
Поэтому
сформулируем задачу иначе: пусть имеется набор линейно-независимых функций 
, которые мы будем использовать при построении пробной
волновой функции Ф:
(V.30).
Подстановка
в (V.30) функционала энергии (V.24) дает:
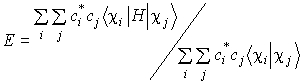(V.31).
Поскольку
функции 
фиксированы, то экстремум
функционала энергии достигается при условии:
(V.32).
Выполняя
дифференцирование (V.31), получим
систему уравнений:
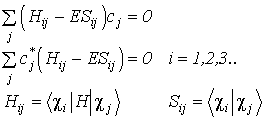(V.33).
Второе
равенство в (V.33) есть
комплексно-сопряженное от первого, поэтому достаточно рассмотреть одно из них,
например - первое. Это есть система линейных алгебраических уравнений, и она
имеет решения, если
(V.34).
Решая
уравнение (V.34), мы можем получить N корней 
, подстановка которых в (V.33)
дает нам наборы коэффициентов 
, т.е. пробные функции 
, отвечающие стационарным точкам функционала энергии.
Изложенный
выше вариант метода называется вариационным методом Ритца. Он имеет одну
замечательную особенность: приближенные значения энергии 
, полученные из уравнения (V.34) являются оценками сверху для соответствующих собственных
значений уравнения Шредингера, т.е. методом Ритца мы можем изучать не только
основное, но и возбужденные состояния квантово-механической системы.
Итак,
мы рассмотрели два основных способа получения приближенных решений уравнения
Шредингера - теорию возмущений и вариационный метод. Каждый из них имеет свои
преимущества и пригоден только для определенного класса задач. Теория
возмущений позволяет работать с весьма простыми функциями, однако имеет тот
недостаток, что для получающихся результатов нет надежного критерия истинности.
Вариационный метод замечателен тем, что в нем точно известно, что чем ниже
энергия, тем мы ближе находимся к точному решению. Однако насколько -
неизвестно. Кроме того, этот метод существенно более сложен с вычислительной
точки зрения.