1.1. Первопринципные методы расчета

Наиболее удобным, с точки зрения квантовой химии, является такой метод расчета структуры и свойств молекул, который использовал бы информацию только о конфигурации электронных оболочек атомов, составляющих систему. Реализация такого метода позволила бы исследователям предсказывать существование и свойства новых материалов, еще не полученных в эксперименте, например, сверхтвердых материалов и др. [1].

Ab initio, т. е. первопринципные методы, используют вышеописанный принцип, однако из-за высокой сложности расчета в них также применяются некоторые приближения, которые не позволяют применить эти методы к любым системам. При этом точность расчета в большинстве случаев довольно высока. Так, например, в [2] были успешно предсказаны структура и свойства внутреннего ядра Земли, состоящего в основном из железа.

К основным методам расчета из первых принципов можно отнести следующие:

• метод Хартри-Фока и его дальнейшие развития;
• метод функционала электронной плотности.

1.1.1. Метод Хартри

Фока

1.1.1.1. Уравнение Хартри

Фока

Метод Хартри Фока, или метод самосогласованного поля, является одним из эффективных методов решения задач квантовой химии. Его идея состоит в том, что взаимодействие электрона с его окружением заменяется взаимодействием с неким усредненным полем . Таким образом, не решаемая квантовомеханическая задача многих тел сводится к решению одночастичного уравнения[1] (где Δ   оператор Лапласа).

Для начала запишем уравнение Шредингера:

(1.1)

где Ψ   многоэлектронная волновая функция рассматриваемой системы.

В теории Хартри многоэлектронная волновая функции представлялась в виде простого произведения одноэлектронных волновых функций

(1.2)

где ψ_p(ξ_i)   нормированная одноэлектронная волновая функция для i-го электрона, находящегося на p-й орбитали, ξ_i   обобщенные координаты, включающие в себя пространственную и спиновую часть. Уравнение (1.2), конечно же, не отражает действительную ситуацию, поскольку электроны являются фермионами, а волновая функция (1.2) не подчиняется принципу Паули. Слэтер (Slater) в [3] видоизменил вид (1.2) и переписал волновую функцию в виде следующего детерминанта:

(1.3)

Записанная в таком виде волновая функция подчиняется принципу Паули. Видно, что если два электрона обладают одинаковыми обобщенными координатами, общая волновая функция системы становится равной нулю. Одноэлектронные волновые функции в (1.3) также включают в себя спиновую часть.

Если система состоит только из спаренных электронов (система с замкнутыми оболочками   closed-shell system), то уравнение (1.3) удобно переписать в следующем виде:

(1.4)

где α и β обозначают спины, направленные вверх и вниз соответственно [4].

Системы с нечетным числом электронов являются системами с незамкнутыми (открытыми) оболочками (open-shell system). В этом случае в уравнении волновой функции (1.4) каждой спиновой координате соответствует своя пространственная координата.

В случае нормированной волновой функции Ψ энергию системы можно выразить следующим образом:

(1.5)

Для построения уравнений Хартри Фока рассмотрим двухэлектронный атом с зарядом ядра Z, в этом случае многоэлектронная функция (1.3) будет иметь следующий вид:

(1.6)

Выражение (1.5), таким образом, может быть записано в следующем виде:

(1.7)

Гамильтониан двухэлектронного атома включает в себя следующие члены:

(1.8)

где H_i   гамильтониан взаимодействия i-го электрона с ядром,    оператор электростатического взаимодействия между первым и вторым электронами.

Энергия двухэлектронного атома в соответствии с (1.5) будет равна

.

(1.9)

Рассмотрим каждый член выражения (1.9) в отдельности. Для члена   можно записать

(1.10)

Преобразуем это выражение и выделим в нем интегралы по координатам индивидуальных электронов. Учитывая при этом ортонормированность одноэлектронных волновых функций, получим

(1.11)

Подобное выражение получается для второго члена из (1.9):

(1.12)

Учитывая тождественность электронов, видим, что первый и второй члены в (1.11) равны соответственно первому и второму членам в (1.12). Следовательно,

(1.13)

Аналогично можно найти, что

(1.14)

В случае последнего слагаемого в (1.9) нельзя разделить на одноэлектронные члены. Вычисляя его ожидаемое значение с антисимметричной волновой функцией и делая очевидные преобразования, получим

(1.15)

Подставляя выражения (1.13) (1.15) в (1.9), находим для ожидаемого значения гамильтониана

(1.16)

Первый и второй члены в этом выражении описывают кинетическую энергию электронов, находящихся на орбиталях ψ₁ и ψ₂ соответственно, третий и четвертый 
взаимодействия этих электронов с ядром, пятый член (кулоновский интеграл) описывает электростатическое отталкивание между двумя электронами, один из которых находится на орбитали ψ₁, а второй   на орбитали ψ₂. Шестой член описывает обменное взаимодействие (обменный интеграл). Распределение заряда для первого электрона описывается произведением , аналогичное выражение дает распределение заряда для второго электрона. Этот член обусловливает различие в энергии между синглетным и триплетным состояниями двухэлектронной системы.

Функция ψ_μ(ξ_i), как уже было сказано выше, включает в себя пространственные и спиновые координаты i-го электрона. Оператор   воздействует только на пространственные координаты. Поэтому вследствие ортогональности различных спиновых функций обменный интеграл отличается от нуля только в том случае, если две входящие в него спиновые функции совпадают. Этот интеграл всегда положителен, поскольку описывает электростатическое отталкивание, но он входит в выражение (1.16) с отрицательным знаком. Следовательно, если спины электронов одинаковы, то вычисленная энергия двухэлектронного атома при заданных пространственных частях функций ψ₁ и ψ₂ оказывается ниже, чем в случае, когда спины электронов различаются. Триплетные состояния соответствуют наличию у электронов одинакового спина. И поэтому из двух спиновых состояний, возникающих в двухэлектронной системе, они характеризуются более низкой энергией, что согласуется с правилом Хунда.

Обобщим (1.16) на случай многоэлектронного атома. В обобщенное выражение должны войти члены, которые описывают кинетическую энергию и притяжение электронов к ядрам и включают одноэлектронную волновую функцию на каждой занятой спин-орбитали и, кроме того, кулоновский и обменный интегралы для каждой пары электронов. Результирующее выражение имеет вид

(1.17)

где

(1.18)

Выражение (1.17) служит отправной точкой для получения уравнений самосогласованного поля Хартри Фока. Процедура их вывода заключается в том, чтобы минимизировать выражение (1.17) путем варьирования орбиталей, соблюдая при этом требование, чтобы одноэлектронные орбитали были ортонормированы. Используем для этого метод множителей Лагранжа, позволяющий находить экстремум функции многих переменных (см. приложение 1). Варьируемая величина представляется в виде суммы рассматриваемой функции и произведений каждого ограничительного условия на неопределенный (постоянный) множитель. Вариация этой суммы считается равной нулю. В данном случае ограничительными условиями являются требования нормированности каждой орбитали и ортогональности каждой пары орбиталей. Таким образом, варьируемую величину следует записать в виде , где λ_μν   множители Лагранжа. Варьируя это выражение по одной из орбиталей, например по ψ_μ(ξ₁), получим

(1.19)

В уравнении (1.19) явно выписанные члены получаются при наличии функции ψ_μ в левой части интеграла, а соответствующие комплексно-сопряженные члены появляются, если функция ψ_μ оказывается в правой части интеграла. В результате суммирования по μ остается только один член, содержащий индекс μ. Суммирование по ν остается и не распространяется только на члены . Волновые функции можно сконструировать так, что из этих членов останутся только те, в которых ν = μ.

Теперь, чтобы минимизировать рассматриваемую функцию, следует принять, что выражение (1.19) равно нулю. Если сумма функции и комплексно-сопряженной ей величины должна быть равна нулю, то каждая из них порознь тоже должна быть равна нулю. Следовательно, можно записать

(1.20)

Запишем третий член уравнения в интегральной форме:

(1.21)

Умножив и разделив выражение (1.21) на произведение , получим:

(1.22)

где    обменный оператор. Если выражение назвать кулоновским оператором, обозначив его символом , то уравнение (1.20) можно переписать в виде:

(1.23)

Заменив величину λ_μμ на ε_μ, а сумму операторов в скобках   на   (оператор Фока или фокиан), получим псевдоуравнение (нелинейное уравнение) на собственные значения:

(1.24)

Оператор Фока можно построить для каждой занятой одноэлектронной орбитали системы. Псевдоуравнения на собственные значения могут быть решены для каждой орбитали. Однако оператор Фока содержит операторы и , зависящие от распределения всех электронов, кроме того электрона, который описывается данным уравнением на собственные значения. Такое уравнение необходимо решать с помощью итерационной процедуры самосогласования [5].

В случае системы с замкнутыми электронными оболочками оператор Фока имеет следующий вид:

(1.25)

где коэффициент 2 появляется из-за суммирования по спиновым переменным.

1.1.1.2. Базисные функции

На практике для решения уравнения (1.24) необходимо представлять молекулярную орбиталь (волновую функцию исследуемой системы) в виде комбинации атомных орбиталей (АО) (волновых функций атомов, входящих в систему), которые в свою очередь представимы как линейная комбинация конечного числа базисных состояний χ_p:

(1.26)

Выбор базисных атомных функций является важной задачей, так как именно он определяет, насколько точно разложение (1.26) аппроксимирует молекулярную орбиталь Хартри Фока. Этот ряд должен достаточно быстро сходиться, т. е. малое число атомных орбиталей должно аппроксимировать молекулярную орбиталь с требуемой точностью. Существует три основных критерия для выбора базисных функций:

1.      Базисные функции должны давать в основном хорошее приближение к истинной волновой функции (например, возле ядер и на больших расстояниях от них).

2.      Базисные функции должны допускать аналитическое вычисление нужных интегралов.

3.      Полное число базисных функций не должно быть очень большим [6].

На данный момент широко используются следующие наборы базисных функций:

Ø      плоские волны ;

Ø      слэтеровские орбитали ;

Ø      гауссовы орбитали ;

Ø      численные орбитали, форма которых оптимизируется из атомных расчетов.

Разложение по плоским волнам описывает обычно с хорошей точностью расчет электронной структуры периодичной кристаллической структуры. Также это разложение может быть успешно применено для расчета аморфных тел и/или конечных систем, таких как атомные кластеры или структуры с дефектами. С математической точки зрения, только плоские волны формируют полный базисных набор, т.е. при увеличении числа базисных функций точность решения уравнения Фока также будет увеличиваться.

Херрингом (Herring) [7] предложен метод ортогонализованных плоских волн (ОПВ)   Orthogonalized Plane Waves (OPW). Он обратил внимание на тот факт, что медленная сходимость ряда (1.26) связана с сильными осцилляциями волновых функций электронов проводимости в области сердцевины иона (см. также метод псевдопотенциала). В этой области волновые функции очень похожи на атомные волновые функции валентного электрона. Чтобы воспроизвести такие осцилляции в методе плоских волн, необходимо было бы строить разложение из огромного числа (   ) плоских волн. Сходимость можно улучшить, только если каким-то образом учесть эти осцилляции в самом базисе, по которому мы будем разлагать функции.

Именно это и сделал Херринг, воспользовавшись тем, что волновые функции, которые требуется найти, должны быть ортогональны волновым функциям внутренних оболочек (последние считаются известными). Таким образом, полное разложение для волновых функций зоны проводимости можно получить, если пользоваться не просто плоскими волнами, а плоскими волнами, которые предварительно были сделаны ортогональными к волновым функциям внутренних оболочек. В процессе ортогонализации учитываются осцилляции в области сердцевины ионов, что позволяет в дальнейшем достаточно хорошо описать и соответствующие осцилляции в волновых функциях, которые мы ищем. Следовательно, этот метод очень похож на метод плоских волн, но только в нем вместо обычных плоских волн фигурируют ортогонализованные плоские волны.

Запишем ортогонализованную плоскую волну в виде

(1.27)

где    нормированная собственная функция внутренних оболочек, индекс t   характеризует состояние внутренних оболочек (1s, 2s, 2p, …), а индекс j   указывает на положение иона; Ω   нормированный объем (объем кристалла).

В том, что ОПВ действительно ортогональны функциям внутренних оболочек, можно убедиться, если умножить выражение для них слева на какую-нибудь из этих функций и проинтегрировать. Интеграл оказывается равным нулю, если мы предположим, что волновые функции внутренних оболочек, относящиеся к различным ионам, не перекрываются (что на самом деле является хорошей аппроксимацией), а также учтем ортогональность таких функций, отвечающих различным состояниям одного иона. Таким образом, они образуют полную систему для разложения функций зоны проводимости, и именно это важно.

Несколько ранее Слэтер [8] предложил в качестве базиса для разложения волновых функций другой тип функций   так называемые присоединенные плоские волны (ППВ) (augmented plane waves   APW). Прежде чем начать конструировать эти функции, целесообразно сначала выбрать какую-то аппроксимацию для потенциала, который будет использоваться в расчетах. Можно ожидать, что вблизи каждого ядра потенциал будет, скорее всего, сферически симметричным (радиус сфер должен быть достаточно малым, чтобы потенциалы, отвечающие различным атомам, не перекрывались), а в пространстве между сферами положим потенциал равным некоторой константе (рис. 1-1).

Присоединенные плоские волны определяются следующим образом: в пространстве между сферами волновые функции представляют собой плоские волны. В интересующей нас области энергий мы строим также решения для сферически симметричного потенциала. Коэффициенты перед этими функциями подбираются таким образом, чтобы волновая функция на поверхности сферы, переходя в плоскую волну, не испытывала скачка. Однако избежать таким образом разрывности первой производной не удается. Собственные функции электронов, отвечающих данной энергии, могут быть точно разложены по таким ППВ. При этом ППВ заменяют в расчетах плоские волны или ОПВ. Как и в случае ОПВ, требуется лишь ограниченное число членов суммы, и поэтому для расчета энергетических зон метод ППВ является очень эффективным [9].

Рассмотрим теперь базисы гауссовых и слэтеровских орбиталей, которые применяется, в основном, для расчета конечных тел   кластеров и отдельных молекул.

Слэтеровские орбитали являются наиболее естественными, если расчет начинается с изолированных атомов, так как функции слэтеровского типа являются точным решением водородоподобного атома. Однако некоторые интегралы кулоновского типа не могут быть решены аналитически при использовании этого набора.

В квантово-химических расчетах большее распространение получили простейшие виды атомных орбиталей слэтеровского типа   АО Слэтера Зенера

(1.28)

Здесь

(1.29)

 нормированные вещественные сферические гармоники, где

(1.30)

 присоединенные полиномы Лежандра, δ_m равно 2 при m = 0 и равно 1 в остальных случаях.

Параметрами орбиталей (1.28) являются квантовые числа n, l и m, показатели экспоненты ζ и координаты точек центрирования орбиталей. Обычно для базисных функций используются квантовые числа, соответствующие занятым и ближайшим возбужденным состояниям электрона в атоме. В целях сокращения количества молекулярных интегралов можно включать в базисный набор только орбитали с главными квантовыми числами, не превосходящими главного квантового числа n для заполненных оболочек в атоме (минимальный базис). В ряде случаев (полуэмпирические методы) в базис включаются только валентные орбитали (валентное приближение).

Для определения ζ Слэтер в 1930 году предложил набор эмпирических правил, основанных на стремлении к наилучшему воспроизведению первых потенциалов ионизации атомов. Согласно этим правилам

(1.31)

где Z   заряд ядра, n*   эффективное (возможно, дробное) главное квантовое число, S   константа экранирования, определяемая следующим образом.

1.      Все электроны в атоме делятся на группы: 1s; 2s, 2p; 3s; 3p; 3d; 4s, 4p; 4d; 4f; и т. д.

2.      S равно сумме следующих вкладов:

·        0 для любых электронов, расположенных во внешних группах;

·        0,35 от каждого электрона в группе, кроме рассматриваемого (0,30 в случае 1s-группы);

·        для s- и p-электронов по 0,85 от каждого электрона с главным квантовым числом, на единицу меньшим, чем у рассматриваемого, и по 1,00 от каждого электрона следующих внутренних оболочек;

·        для d- и f-электронов по 1,00 от каждого электрона, расположенного во внутренних группах.

Радиальные функции слэтеровского типа недостаточно точно описывают поведение атомных орбиталей Хартри Фока на небольших расстояниях от ядра. Этот недостаток устраняется аппроксимацией каждой из этих АО, по крайней мере, двумя слэтеровскими функциями с разными орбитальными экспонентами

(1.32)

Функции (1.32) называются дубль-зета-функциями, а соответствующий базисный набор   дубль-зета-базисом (DZ, широкое применение имеет также трипл-зета-базис 
TZ).

Квантово-химические расчеты с использованием слэтеровских функций в качестве базисных орбиталей являются достаточно сложными и трудоемкими. Гауссовы орбитали частично решают эту проблему, но иногда при этом разложении также необходимо достаточно большое число членов в ряду (1.26).

В 1950 году С. Ф. Бойс предложил использовать базисные функции гауссова типа, имеющие вид

(1.33)

Их основное отличие от слэтеровских функций (1.28) заключается в квадратичной зависимости от r аргумента экспоненты. Это позволяет представлять произведения гауссовых функций (центрированных в разных точках), встречающиеся в многоцентровых интегралах, в виде линейной комбинации одиночных гауссовых функций, центрированных в общем случае в другой точке пространства. В результате сильно упрощаются вычисления всех интегралов.

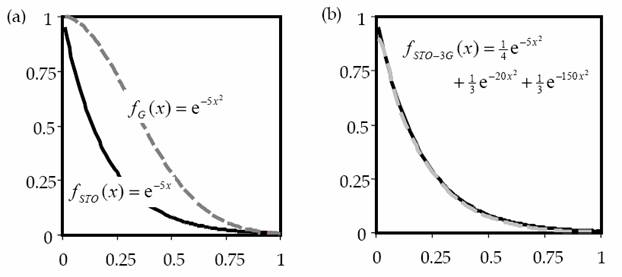
Одна слэтеровская АО аппроксимируется обычно несколькими гауссовыми функциями. Поэтому базис гауссовых функций всегда больше базиса слэтеровских АО (Рис. 1-2).

Рис. 1-2. Сравнение экспоненциальной и гауссовой функции (а) и той же экспоненциальной функции и комбинации трех гауссовых функций [10] (b).

Наиболее простым типом базисных наборов является ОСТ-nГФ (STO-nG), где каждая атомная орбиталь состоит из суммы n (обычно от двух до шести) функций гауссова типа, причем коэффициенты гауссовых функций подобраны таким образом, чтобы их линейные комбинации приближенно описывали поведение орбиталей слэтеровского типа. Проведение тестовых расчетов с использованием этих базисных наборов показало, что при n ≥ 3 результаты расчетов очень схожи. Поэтому наиболее широкое распространение получил минимальный базисный набор ОСТ-3ГФ (STO-3G). Минимальные базисные наборы включают только атомные орбитали, которые необходимы для размещения электронов нейтрального атома. Сферическая симметрия атомов и пространственная инвариантность молекул требуют включение всех трех типов np-орбиталей при появлении хотя бы одного p-электрона.

Малый размер и простота базиса ОСТ-3ГФ являются основными причинами его недостатков (неудовлетворительные результаты расчетов соединений электроположительных элементов третьего периода, переоценка стабильности малых циклов и π-акцепторной способности электроположительных элементов второго периода), которые устраняются при использовании более широких валентно-расщепленных и биэкспоненциальных базисов (DZ). В этих базисах АО составлены из двух частей   внутренней, более компактной, и внешней   более диффузной. При построении МО в процессе ССП коэффициенты каждой из орбиталей этих двух типов можно варьировать независимо.

В валентно-расщепленных базисных наборах на компактную и диффузную составляющие разделены только валентные орбитали. Поэтому схема записывается как m-npГФ (m-npG), где m   число гауссовых функций, заменяющих каждую внутреннюю АО, n и p   число гауссовых функций с разными значениями экспонент, аппроксимирующих каждую валентную АО. Наиболее часто применяемым является базис 6-31ГФ (6-31G). В биэкспоненциальных базисах (как указывалось выше) расщеплены как валентные, так и внутренние орбитали остова.

Для улучшения описания молекулярных орбиталей на больших расстояниях от ядра часто используют базисные наборы с включением поляризационных функций. Поляризационные функции   дополнительные волновые функции с l + 1, где l   орбитальное квантовое число последних заполненных атомных орбиталей. Одними из наиболее используемых поляризационных базисных наборов являются 6-31ГФ* и 6-31ГФ**, где звездочка обозначает добавление поляризационных d-функций к p-элементам (или f-функций к d-элементам). Вторая звездочка обозначает добавление поляризационных p-функций к 1s-орбиталям атомов водорода.

Для расчетов молекул, требующих более точного описания несвязывающих электронных пар, в базисные наборы вводятся специальные диффузные s- и p-функции со значениями экспонент от 0,1 до 0,01. Их включение обозначается знаком «+», например
3-21+ГФ.

Выбор базиса, подходящего для решения задачи, определяется стремлением получить более точное решение, с одной стороны, и ограничениями, связанными с ресурсами ЭВМ, с другой. Поэтому на практике применяется часто схема, когда полная оптимизация выполняется с использованием небольших базисов, после чего в более широких базисах проводятся расчеты для одной геометрической конфигурации и устанавливаются поправки, связанные с учетом электронной корреляции [11].

1.1.1.3. Уравнения Хартри

Фока

Рутана

Базисные функции гауссова и слэтеровского типа, локализованные на разных атомах, не ортогональны друг другу:

(1.34)

здесь R₁ и R₂   радиус-векторы первого и второго атомов.

Пусть в качестве базисного набора выбран ряд таких неортогональных функций. Уравнение Фока будет записано в следующем виде:

.

(1.35)

Домножив это уравнение на   и проинтегрировав, получим (в матричной форме записи)

,

(1.36)

где F   матрица оператора Фока, S   матрица перекрытия для базисных функций, определяемые следующим образом:

.

(1.37)

Часто уравнение (1.36) записывают в следующем виде:

.

(1.38)

Обобщенное уравнение на собственные значения (1.36) или (1.38) называется уравнением Рутана (Ruthan).

Матрица оператора Фока в случае системы с замкнутыми оболочками, таким образом, имеет следующий вид:

,

(1.39)

где

,	(1.40)
.	(1.41)

Индекс k обозначает орбиталь _k, а p, q, r, s   базисные функции. Суммирование по k идет по всем занятым орбиталям.

Введем следующее обозначение:

.

(1.42)

P_rs называется матрицей плотности. Таким образом, матрица Фока может быть переписана в следующем виде:

(1.43)

С помощью унитарного преобразования обобщенное уравнение на собственные значения может быть приведено к обычному уравнению на собственные значения

,

(1.44)

где

,

(1.45)

и матрица V трансформирует S в единичную матрицу:

.

(1.46)

1.1.1.4. Алгоритм расчета с помощью метода Хартри

Фока

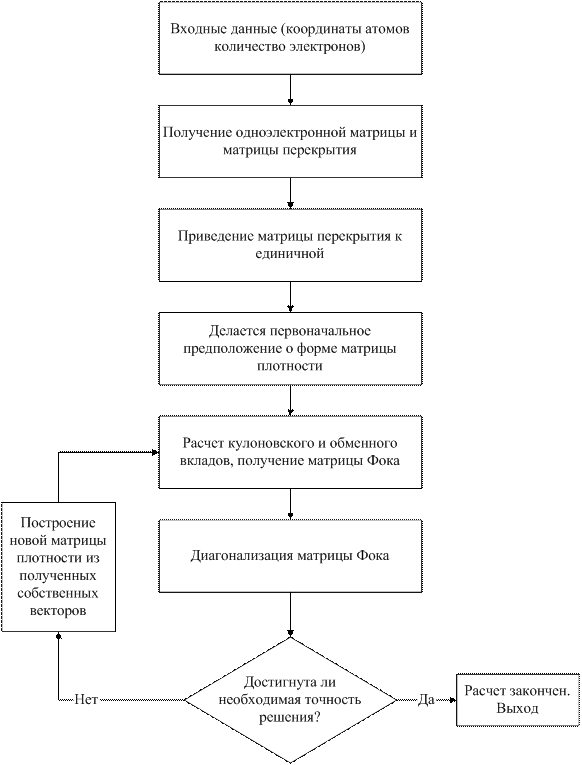
На следующей блок-схеме представлен алгоритм расчета с помощью метода Хартри Фока (рис. 1-3).

Рис. 1-3. Блок-схема алгоритма расчета с помощью метода Хартри Фока.

Входные данные: В качестве входящих данных задаются координаты атомов, заряды ядер, полное число электронов и базисные функции.

Получение матриц: Получение матриц, не зависящих от собственных векторов (матрица перекрытия S_pq, матрица одноэлектронного гамильтониана H_pq, двухэлектронные интегралы   ).

Приведение матрицы перекрытия к единичной: Расчет матрицы V_pq (см. (1.45)).

Диагонализация матрицы Фока: Используя матрицу V_pq, решается обобщенное уравнение на собственные значения (1.36).

Построение новой матрицы плотности: Используя полученные собственные векторы, строится новая матрица плотности [12].