Глава III.3.
Природа химической связи в фуллеренах
Для изучения природы данного химической связи в фуллеренах необходимо рассмотреть подробнее электронную структуру молекулы С60. Наибольший интерес представляет собой потолок валентной зоны данного соединения. Целесообразно рассматривать структуру электронных уровней фуллерена С60 в сравнении со структурой молекул обладающими p-системой, например бензола, антрацена, пирина и т.п (Рис. 3.1).
|
|
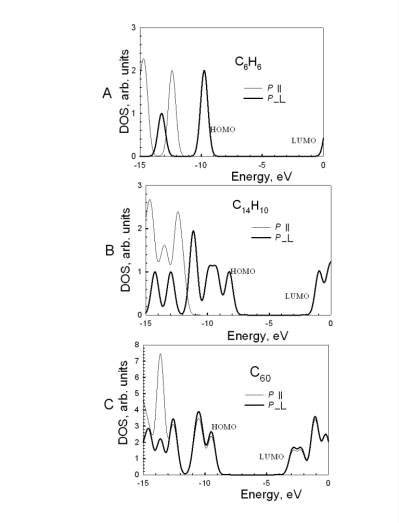
Рисунок 3.1. а) Парциальные электронные плотности состояний для молекулы C6H6; b) Парциальные электронные плотности состояний для молекулы С10Н10, c) Парциальные электронные плотности состояний для молекулы С60; Жирными линиями нарисованы вклады p-связей (^), а тонкими - s (||). Видно четкое разделение этих состояний в традиционной ароматике и смешивание – в молекуле фуллерена. |
Молекулярные уровни в бензоле делятся на два вида: s характера (p||), в которых присутствуют смешанные вклады от атомных px, py и s орбиталей углерода и водорода и состояния p типа, сформированные только pz орбиталями углерода (p^). Анализ парциальных плотностей состояний показывает четкое разделение соответствующих пиков для p-системы, представленной двумя максимумами, и всех остальных уровней (Рис. 3.1a). С увеличением числа атомов в молекуле (антрацен, пирин) количество пиков, соответствующих p-системе, возрастает. При этом расположение энергетических уровней и их природа существенно не меняется (Рис. 3.1b).
Вследствие кривизны поверхности молекулы С60 происходит перекрывание атомных орбиталей, лежащих в плоскости поверхности молекулы (p||) и атомных орбиталей, располагающихся по нормали к молекулярной поверхности (p^). В результате в фуллерене отсутствуют уровни, имеющие четко выраженный s или p характер, свойственные плоским молекулам (Рис. 3.1c). При этом для систем с различным зарядом на углеродной части комплекса соотношение вкладов p^ электронов и и p|| электронов в уровни потолка валентной зоны изменяется (Таблица 1).
Таблица 1
|
Углеродный кластер |
Отношение p^ / p|| в HOMO |
|
|
1.11 |
|
|
0.65 |
|
|
0.98 |
|
|
0.92 |
|
|
1.19 |
|
|
0.84 |
Для молекулы С60
величина отношения вкладов p^ / p|| в HOMO-орбитали составляет 1.1.
При изменении заряда системы отношение p^ / p||
уменьшается, за исключением кластера ![]() с мультиплетностью
равной единице. Очевидно, что соотношение вкладов p^ и p|| электронов в уровне определяет и его природу.
с мультиплетностью
равной единице. Очевидно, что соотношение вкладов p^ и p|| электронов в уровне определяет и его природу.
Добавление дополнительных электронов или образование электронных вакансий на углеродной сфере приводит к существенному изменению относительных вкладов p^ и p|| электронов во всю электронную структуру (Рисунок 3.2). Как видно из рисунка, любое изменение количества электронов в системе приводит лишь к одному эффекту – к увеличению s-компоненты, что и определяет изменение всех физических свойств производных фуллерена.
|
|
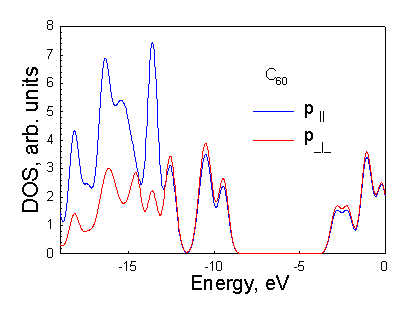
Рисунок 3.2. (а) Плотности p^ и p|| состояний молекулы С60. Видно, что вклад p^ состояний в потолок валентной зоны и дно зоны проводимости превышает вклад p|| состояний. |
|
|
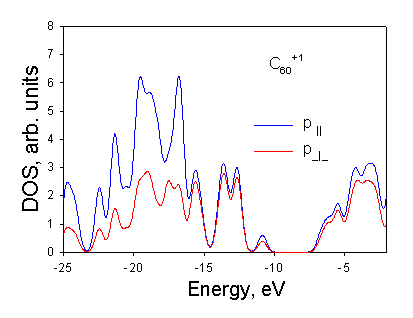
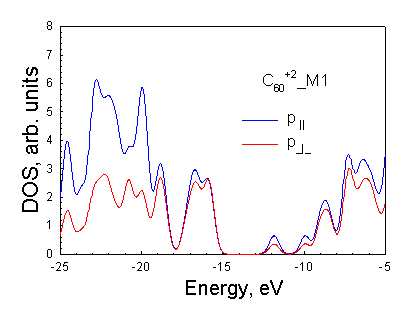
Рисунок 3.2. (б) Плотности p^ и p|| состояний молекулы С60+. Видно, что вклад p^ состояний в потолок валентной зоны и дно зоны проводимости стал меньше вклада p|| состояний. |
|
|
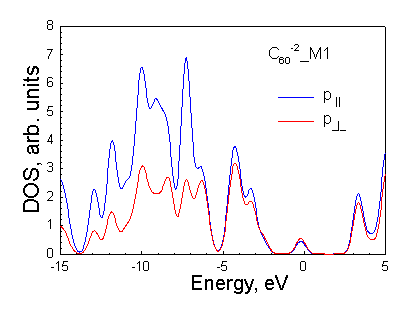
Рисунок 3.2. (в) Плотности p^ и p|| состояний молекулы С60-2 (полный спин S=0). Видно, что вклад p^ состояний в потолок валентной зоны и дно зоны проводимости стал меньше вклада p|| состояний. |
|
|
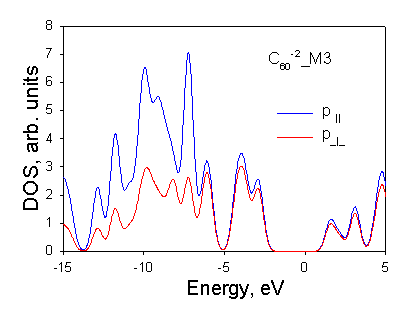
Рисунок 3.2. (е) Плотности p^ и p|| состояний молекулы С60-2 (полный спин S=1). Видно, что вклад p^ состояний в потолок валентной зоны и дно зоны проводимости стал меньше вклада p|| состояний. |
|
|
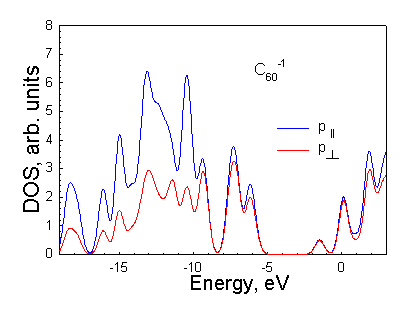
Рисунок 3.2. (д) Плотности p^ и p|| состояний молекулы С60-1. Видно, что вклад p^ состояний в потолок валентной зоны и дно зоны проводимости стал меньше вклада p|| состояний. |
|
|
Рисунок 3.2. (е) Плотности p^ и p|| состояний молекулы С602 (полный спин S=0). Видно, что вклад p^ состояний в потолок валентной зоны и дно зоны проводимости стал меньше вклада p|| состояний. |
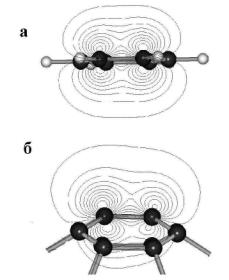
Еще более очевидными становятся отличия в в электронной структуре фуллерена и плоских ароматических систем после анализа карт электронных плотностей орбиталей, например – верхней заполненной орбитали (Рисунок. 3.3).
|
|
Рисунок. 3.3. Пространственное распределение верхней заполненной орбитали в молекуле С6Н6 (а) и С60 (б) |
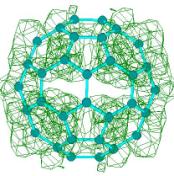
Как видно из рисунка, основным отличием является изменение пространственной симметрии орбиталей за счет примешивания s-компоненты в p-систему, что выражается в пространственном «поджимании» электронного облака, расположенного внутри углеродного полиэдра и, наоборот, «расплывании» той части, которая находится снаружи фуллерена.
Для того, чтобы более полно
понять природу химической связи в фуллеренах рассмотрим другие
высокосимметричные замкнутые молекулы Сn (n=20,
36, 60, 80, 180, 240). Низший фуллерен C20 имеет симметрию икосаэдра Ih (C20-M1.hin),
C36 –
симметрии D2d (c36_d2d.hin),
D3h (c36_d3h.hin)
и D6h (c36_d6h.hin),
C60 –
симметрию Ih
(C60.hin), C80 - симметрию Ih (C80.hin), C180 - симметрию Ih (C180.hin) и C240 - симметрию Ih (C240.hin). Все
молекулы фуллеренов представляют собой замкнутую поверхность,
образованную пяти- и шестиугольниками. Пятиугольник, встроенный в графитовую
плоскость, индуцирует ее искривление на 30Å,
поэтому во всех таких структурах имеется 12 пятиугольников, что обеспечивает
замкнутую поверхность, и n шестиугольников. Таким образом, все эти молекулы
отличаются друг от друга количеством шестиугольников.
Увеличение числа шестиугольников в ряду исследуемых кластеров приводит к изменению их геометрической формы. В фуллерене С60 атомы углерода, занимающие вершины шестиугольника располагаются в одной плоскости. В фуллеренах с большим числом атомов, шестиугольники, образующие поверхность молекулы, искажаются. Отклонение вершин многоугольника от плоскости описывается величиной соответствующего торсионного угла.
В С60
торсионные углы для атомов - вершин шестиугольника равны нулю. Увеличение
размеров кластера казалось бы должно приводить к менее напряженной структуре
молекул. Однако фуллерен С60 занимает особое положение в ряду
углеродных кластеров. Каждый из многоугольников, образующих поверхность
молекулы располагается на отдельной грани пространственной фигуры. В молекулах
других фуллеренов ребра фигуры проходят через шестиугольники, обуславливая их
искажение. При этом пятиугольники по-прежнему остаются на отдельной грани,
вследствие чего они не подвержены искажениям. В кластере С80
максимальное значение величины торсионных углов в шестиугольниках составляет
2.90. В молекуле С180 она увеличивается до 8.90.
Относительно большие размеры фуллерена С240 приводят к появлению в его
структуре неискаженных шестиугольников, расположенных целиком на гранях
пространственной геометрической фигуры. Однако остальные углеродные
шестиугольники, пересекающиеся с ребрами пространственного многоугольника,
претерпевают более сильное искажение в сравнении с другими изучаемыми
кластерами (величина максимального торсионного угла составляет 14.50).
Интересно сравнить электронную структуру всех вышеперечисленных высокосимметричных фуллеренов (Рис. 3.4)
а
|
б
|
|
в
|
г
|
|
д
|
е
|
|
ж
|
з
|
|
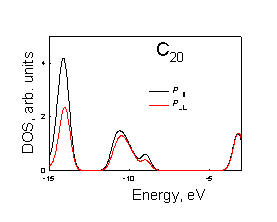
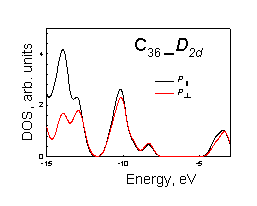
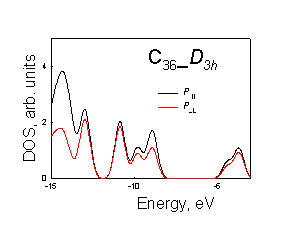
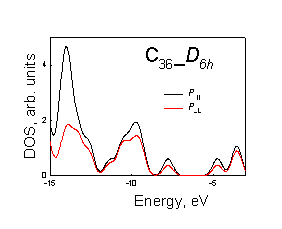
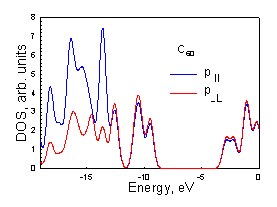
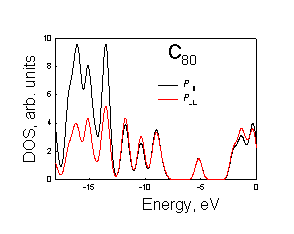
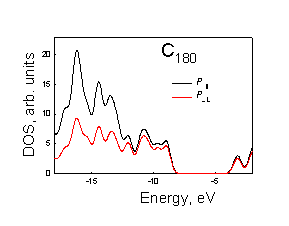
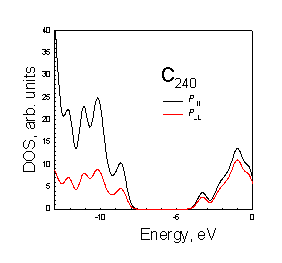
Рисунок. 3.4. Плотности p^ и p|| состояний молекул фуллеренов: а) – С20, б) – С36 D2d, в) – C36 D3h, г) С36 D6р, д) С60, е) C80, ж) C180, з) C240 |
|
В молекуле С60
в верхнем заполненном уровне преобладает вклад от p^ атомных орбиталей.
Величина отношения вкладов p^: p|| в верхнее заполненное состояние
составляет ~1.1. В молекулах других
фуллеренов искажение шестиугольников приводит к понижению перекрывания p^ атомных
орбиталей между собой и их большему взаимодействию с орбиталями расположенными
тангенциально к поверхности, что приводит к уменьшению вкладов от орбиталей p^ в верхнее
заполненное состояние.
Таким образом, по мере увеличения величины торсионного угла (увеличивается искажение углеродных шестиугольников, образующих поверхность молекулы фуллерена) уменьшается вклад в вернее заполненное состояние атомных орбиталей направленных перпендикулярно к молекулярной поверхности (Рис 3.4).
Для того, чтобы убедится, насколько корректно квантово-химические расчеты воспроизводят формы электронных облаков и, следовательно, корректности сделанного вывода о деформации электронных облаков можно провести сравнение теоретических (полученных полуэмпирическим методом РМ3) и экспериментальных [1] карт полной электронной плотности, фолновых функций и квадратов волновых функций HOMO и LUMO (Рисунок. 3.5).
|
А)
STM-карта полной электронной
плотности С60 |
Карта полной электронной плотности (PM3-метод) |
|
|
Б)
STM-карта полной плотности HOMO-орбитали С60 |
|
|
|
В)
STM-карта полной плотности LUMO-орбитали С60 |
Карта электронной плотности LUMO-орбитали (PM3-метод) |
Карта LUMO-орбитали(PM3-метод) |
|
Рисунок 3.5. Экспериментальные [1] и теоретические карты электронных плотностей. А) карта полной электронной плотности, б) карта плотности HOMO, в) карта плотности LUMO |
||
Как видно из этих рисунков, экспериментальные и теоретические карты распределения как полной электронной плотности, так и электронной плотности, находящейся на HOMO и LUMO-орбиталях похожи. Необходимо напомнить, что процедура отрисовки карт в работе [1] конкретезирована не была, при этом использовался алгоритм представления электронных облаков в виде изображений с различной оптической плотностью, что не позволяет прямо их сравнивать с картами в виде изолиний, получающихся в квантово-химических методах.
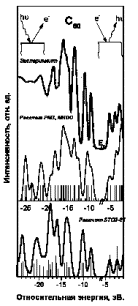
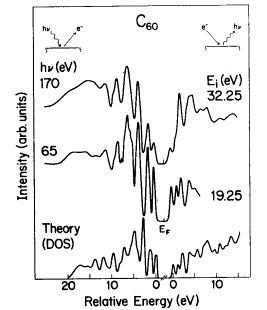
Одним из самых детальных экспериментальных исследований электронной структуры занятых и вакантных электронных состояний С60 является работа [2] (Рисунок. 3.6). В работе была исследована электронная структура занятых и вакантных состояний методом фотоэлектронной спектроскопии и спектроскопии обращенной фотоэмиссии. Там же приводились и результаты квантово-химических расчетов LDA методом.
А
|
Б
|
|
Рисунок 3.6.. А) Экспериментальные фотоэлектронный спектр и спектр обращенной фотоэмиссии [2] и полные плотности состояний, рассчитанные полуэмпирическим методом PM3 и методом Хартри-Фока в базисе 3-21G (наши данные). Б) Экспериментальные фотоэлектронные спектры и спектры обращенной фотоэмиссии, снятые при различных энергиях возбуждения. На нижней кривой изображены теоретические плотности состояний, рассчитанные методом LDA [2]. |
|
Во
всех случаях были получены хорошее соответствие экспериментальных и теоретических
данных, что говорит о том, что квантово-химические методы могут количественно
описывать не только электронные состояния с отрицательными энергиями, но и
состояния фотоэлектронов в континууме.
Таблица 2.
Структурные и электронные
параметры молекулы С60: Длины связей, потенциалы ионизации (IP) и
сродство к электрону (EA). L(S)DA-приближение локальной (спиновой) плотности,
BLYP – метод градиентных поправок Бека-Ли-Янга-Парра, МР2- теорея возмущения
Мёллера-Плессета второго порядка
|
Метод и базис |
Длинна связи (нм) |
IP(v)[IP(ad)] (eV) |
EA(v)[EA(ad)] (eV) |
|
LSDA (базис плоских волн с использованием псевдопотенциала [3]) |
0.1387; 0.1438 |
7.59 [7.55] |
2.90 [2.96] |
|
LDA (TZP-базис, полноэлектронный расчет) [4] |
0.1388; 0.1441 |
- |
- |
|
LDA (LCGTO-базис (11s/7p1d), полноэлектронный расчет) [5] |
0.139; 0.145 |
7.60 |
2.82 |
|
BLYP (расчет псевдопотенциальный в базисе плоских волн) [3] |
0.1401; 0.1459 |
7.08 [7.04] |
2.47 [2.52] |
|
BLYP (расчет полноэлектронный в базисе плоских волн) [3] |
0.1403; 0.1461 |
- |
- |
|
Эксперимент [6] |
0.1401; 0.1458 |
7.6 |
2.65 |
|
Ab initio (TZP-базис) [7] |
0.1370; 0.1448 |
8.0 |
0.65 |
|
Ab initio (6-311G*-базис) [8] |
0.1372; 0.1448 |
- |
- |
|
MP2 (TZP-базис) [9] |
0.1406; 0.1446 |
- |
- |
До настоящего времени в большинстве неэмпирических квантово-химических расчетов молекулы С60 использовались малые базисные наборы из-за сложности системы. Следует обратить особое внимание на то, что корректность, с какой ab initio методы описывают особенности электронной структуры прямо говорит о важности учета корреляционных эффектов. Проведем теперь сравнения теоретических и экспериментальных потенциалов ионизации (IP, v-вертикальный, ad-адиабатический), сродства к электрону (EA, v-вертикальный, ad-адиабатический) и межатомных расстояний в молекуле С60 (Таблица. 2).
Как видно, пренебрежение корреляционными эффектами приводит к заметному уменьшению длинны связей. Такой результат является типичным для метода Хартри-Фока и связан с переоценкой щели между верхней занятой и нижней вакантной орбиталями. Уменьшение длинны связи в большей степени затрагивает связи (6-6). Теория возмущения Мёллера-Плессета второго порядка существенным образом корректирует эти результаты метода Хартри-Фока.
В методе Хартри-Фока самым последовательным методом расчета потенциалов ионизации (IP) и сродства к электрону (EA) является метод DSCF, когда эти величины рассчитываются как разность полных энергий основного и ионизованных состояний. В случае, когда для такого расчета берется геометрия основного состояния, такой потенциал ионизации называется вертикальным, а в случае, когда для ионизованного состояния производится своя оптимизация геометрии – адиабатическим. Как правило, вертикальный потенциал ионизации переоценивается на величину до 0.5 eV, тогда как сродство к электрону существенно недооценивается (Табл. 2). Это говорит о том, что процесс добавления электрона вносит в систему большие корреляционные эффекты, которые и влияют на энергетические характеристики подобных углеродных структур.
Существенное увеличение роли сильных электронных корреляций при добавлении одного избыточного электрона (даже по сравнению со случаем однократно положительно ионизованной системы) понятно – ненулевая кривизна углеродной поверхности приводит к замешиванию компоненты sp3-гибридизации к sp2-гибридизации. Тем не менее, верхний заполненный уровень в молекуле С60 имеет смешанную s-p-природу (отношение парциальных плотностей s и p вкладов (Рис. 3.1, Табл. 1) равно 1.1). Добавление избыточного электрона или образование вакансии приводит к возникновению внедренного электронного состояния (эти процессы будут рассмотрены ниже, в разделах, посвященных электрон-допированным углеродным наноструктурам) и повышению (в большинстве случаев, см. Табл. 1) s-вклада. Известно, что sp3-гибридизация электронных облаков формирует сильно локализованные связи. В случае, когда в системе наблюдается большое количество эквивалентных центров, это приводит к тому, что сильно локализованная sp3-компонента начинает «гулять» по системе, существенным образом меняя электронную структуру.
СПИСОК ЛИТЕРАТУРЫ К ГЛАВЕ III.3.
[1] Бахтизин Р.З., Хашицуме Т., Щ.-Д. Вонг, Сакурай Т., УФН 167, 289 (1997).
[2] Weaver J.H. Acc. Chem. Res. 25, 143 (1992).
[3] Andreoni W., Annu. Rev. Phys. Chem. 49, 405
(1998).
[4] van Wuellen C. Chem. Phys. Lett. 219, 8
(1994).
[5] Dunlop B.I.,
Brenner D.W., Mintmire J.W., Mowrey R.C., White C.T., J. Chem. Phys. 95, 8737
(1991).
[6] Hedberg K., Hedberg L., Bethune D.S., Brown
C.A., Dorn H.C., Science 254, 410 (1991).
[7] Gioslowski J., Electronic Structure
Calculations on Fullerenes and Their Derivatives. New York: Oxford Univ. Press
(1995).
[8] Scuseria G.E., Chem. Phys. Lett. 176, 423
(1991).
[9] Haeser M., Almloef J., Scuseria G.E., Chem.
Phys. Lett. 181, 497 (1991).
 Карта
электронной плотности HOMO-орбитали (PM3-метод)
Карта
электронной плотности HOMO-орбитали (PM3-метод)