Глава I.2.

 

Постулаты квантовой механики и ее математический аппарат

 

Классическая механика и электродинамика при попытке применить их объяснению атомных явлений приводили к результатам, находящихся в резком противоречии с экспериментом. Наиболее яркий тому пример - попытка применения классической электродинамики к модели атома, в которой электроны движутся вокруг ядра по классическим орбитам. При таком движении, как и при всяком движении зарядов с ускорением, электроны должны были бы непрерывно излучать энергию в виде электромагнитных волн и, в конце концов, - неизбежно упасть на положительно заряженное ядро. Таким образом - с точки зрения классической электродинамики - атом неустойчив. Как мы видим - этот тезис не соответствует действительности. Такое глубокое противоречие теории с экспериментом свидетельствует о том, что описание микрообъектов требует фундаментального изменения в основных классических представлениях и законах.

 

Из целого ряда экспериментальных данных (таких, как дифракция электронов) следует, что механика, которой подчиняются атомные явления - квантовая механика - должна быть основана на представлениях о движении, принципиально отличных от представлений классической механики. В квантовой механике не существует понятия траектории частиц, а, следовательно - и других динамических характеристик. ЭТОТ ТЕЗИС СФОРМУЛИРОВАН В ПРИНЦИПЕ НЕОПРЕДЕЛЕННОСТИ ГЕЙЗЕНБЕРГА:

 

 

Следует отметить (и об этом будет говориться позднее), соотношение неопределенностей связывает не только координату и импульс, но и ряд других величин.

 

Известно, что полное описание состояния классической физической системы осуществляется заданием в начальный момент времени всех ее координат и скоростей. По этим данным уравнения движения полностью определяют поведение системы во времени. В квантовой механике, поскольку координаты и соответствующие им скорости не существуют одновременно, описание осуществляется меньшим числом величин, т.е. является менее подробным. Именно поэтому квантовая механика не может делать строго определенных предсказаний относительно будущего поведения микрообъекта, и ее задача состоит лишь в определении вероятности получения того или иного результата при измерении.

 

Естественно, что столь радикальное изменение физических представлений о движении требует и столь же радикального изменения математического аппарата. Основы этого были сформулированы как постулаты квантовой механики:

 

 

В квантовой механике состояние всей системы может быть описано функцией координат Y(q), квадрат модуля которой определяет распределение вероятностей значений координат:

½Y(q)½²dq                       (II.2)

- есть вероятность того, что произведенное над системой измерение обнаружит значение координат в элементе объема dq. Функцию Y(q)  называют волновой функцией системы. Волновая функция обязана удовлетворять ряду требований:

 

а) Она должна быть непрерывной.

б) Она должна быть однозначной.

в) Она должна быть интегрируема с квадратом, т.е. интеграл ò½Y(q)½²dq должен существовать.

г) Она должна быть нормированной, т.е. этот интеграл должен быть равен 1.

 

Физический смысл последнего утверждения довольно прост и прозрачен: сумма вероятностей всех возможных значений координат равна единице, так как обнаружение объекта в любой точке пространства - есть событие достоверное.

 

Следует также отметить, что волновая функция системы может быть комплексной, и она определена лишь с точностью до фазового множителя exp(ia), где a - вещественное число. Эта неопределенность не может быть устранена, однако она несущественна и не отражается на физических результатах.

 

 

 

 

 

Вернемся теперь к рассмотрению математического аппарата квантовой механики.

 

Оператором А принято называть правило, согласно которому каждой функции f соответствует функция j:

 

j= А f           (II.3)

 

Простейшие примеры операторов: извлечение квадратного корня, дифференцирование и т.д.

 

Не на каждую функцию можно подействовать любым оператором, например не дифференцируемую функцию нельзя подействовать оператором дифференцирования. Поэтому любой оператор бывает определен лишь на некотором классе функций и считается заданным, если указано не только правило, по которому он одну функцию преобразует в другую, но и множество функций, на которые он действует.

 

По аналогии с алгеброй чисел можно ввести и алгебру операторов:

 

1)   Сумма или разность операторов

(A ± B)·f =A·f ± B·f            (II.4)

 

2)   Произведение операторов

AB·f=A (B·f)                 (II.5)

 

т.е. сначала на функцию f действует оператор B, образуя некоторую новую функцию, на которую затем действует оператор A. В общем случае действие оператора AB не совпадает с действием оператора BA.

 

Действительно, если A=d/dx и  B=x,

то  AB·f=d/dx(xf)=f+xdf/dx,

 

а BAf=xdf/dx¹f+xdf/dx

 

Если AB=BА, то операторы называются коммутирующими, а если AB-BАº{A,B} (II.6), то они не коммутируют. Выражение в скобках называется коммутатором.

 

В квантовой механике обычно используются линейные самосопряженные (или эрмитовы) операторы. Свойство линейности означает, что

 

A(c₁f₁ + c₂f₂)f= c₁Af₁ + c₂Af₂       (II.7)

 

где c₁ и c₂ - константы, а f₁  и f₂ - произвольные функции, на которых определен оператор A. Это математическое свойство тесно связано с принципом суперпозиции.

 

Самосопряженным эрмитовым оператором называется оператор, для которого выполняется равенство:

òf₁^*(x)(Af₂(x))dx =  òf₂(x)(A^*f₁^*(x))dx  (II.8)

 

при этом предполагается, что A определен на f₁^*(x) и f₂(x) и все интегралы, входящие в (1.8) существуют. Требование эрмитовости очень важно для квантовой механики и ниже мы выясним, почему. 

 

Как уже говорилось, действие оператора сводится к преобразованию одной функции в другую, однако возможны и такие случаи, когда в результате действия оператора исходная функция не изменяется, либо помножается на константу. Простейший пример:

 

 

Можно утверждать, что каждому оператору A можно сопоставить линейное уравнение вида:

 

Af = af       (II.9),

 

где  a = const. a  - собственное значение оператора, а f  - собственная функция оператора. Это уравнение называется уравнением на собственное значение. Значения постоянных, при которых уравнение (1.9) принимает нетривиальные решения, называют собственными значениями. Все вместе они образуют спектр собственных значений, который может быть дискретным, непрерывным или смешанным. Каждому значению соответствует одна или несколько собственных функций f_т, причем если одному собственному значению соответствует только одна функция, то оно является невырожденным, а если несколько - то вырожденным.

 

Собственные функции и собственные значения эрмитовых (самосопряженных) операторов обладают рядом свойств:

 

1.            Собственные значения таких операторов вещественны.

2.            Собственные функции f₁  и  f₂ таких операторов, принадлежащих различным собственным значениям с₁  и  c₂  соответственно ортогональны между собой, т.е. òf₁^*(x)f₂(x)dx = 0   (II.10)

3.            Они должны быть нормированы на единицу введением специального нормировочного множителя, что в общем случае описывается условием ортонормированности: òf_m^*(x)f_n(x)dx = d_mn, d_mn = 0  при m ¹ n  и d_mn = 1  при m = n   (II.11)

4.            Если два оператора  A  и B  имеют общую систему собственных функций, то они коммутируют, справедливо и обратное утверждение

5.            Собственные функции эрмитова оператора образуют полный ортонормированный набор, т.е. любую функцию, определенную в этой же области переменных можно представить в виде ряда по собственным функциям оператора A:

       (II.12),

где  c_n - некоторые константы, и это разложение будет точным.

 

Последнее свойство очень важно для аппарата квантовой механики, поскольку на его основе можно построить матричное представление операторов и применить мощный аппарат линейной алгебры.

 

Действительно, поскольку в (II.12) собственные функции f_n(x)  считаются известными, то для нахождения функции  F(x)  необходимо и достаточно найти все коэффициенты разложения {c_n}. Рассмотрим теперь некоторый оператор B, который действует на функцию  c(x)  и переводит ее в F(x): 

 

F(x) = Bc(x)          (II.13)

 

Представим теперь функции F(x)  и  Bc(x)  в виде рядов (II.12):

 

        (II.14)

 

и подставим их в (II.13)  

 

    (II.15)

 

тогда

 

       (II.16)

 

Помножим обе части равенства на f_k^*(x)  и проинтегрируем, учитывая условия ортонормированности:

 

 

                                   (II.17)

 

Равенство  (II.17) описывает переход от функции  c(x)  к функции F(x), который осуществляется заданием всех коэффициентов M_kn.  Набор всех величин M_kn есть оператор  B в матричном представлении и его можно записать как

 

                     (II.18)

 

Таким образом, любой произвольный оператор B в матричном представлении можно представить в виде квадратной таблицы чисел, матрицы, и это представление будет определятся только видом оператора и исходным набором базисных функций.

 

Вспомним теперь вкратце основные положения теории матриц. Вообще матрицей называется совокупность вещественных или комплексных чисел a_ij , называемыми элементами матрицы,  расположенных в виде прямоугольной таблицы

 

                    (II.19)

 

Индексы i  и  j  показывают, что элемент a_ij   расположен на пересечении i-й строки и j-го столбца. Если матрица имеет  n  строк и  m  столбцов, то говорят, что она имеет размерность (nxm), если  n = m, то матрица называется квадратной. Прямоугольная матрица размера  (1xm)  называется вектор-строкой, а (nx1) - вектор-столбцом. Матричный элемент a_ij  при  i = j  называется диагональным, матрица, в которой все элементы, кроме диагональных, равны нулю называется диагональной, а диагональная матрица, в которой все элементы равны единице - единичной. Сумма диагональных элементов называется следом: Sp.

 

Легко построить алгебру матриц, которая будет сводится к следующим правилам:

 

1.              Матрицы  и  называются равными, если для всех i  и  j  справедливо равенство: a_ij = b_ij

2.              Суммой матриц  и  размерности  (nxm)  будет матрица   размерности  (nxm)  такая, что для всех i  и  j  справедливо равенство: c_ij = a_ij + b_ij

3.              Произведением матрицы   на произвольное число a будет матрица   такой же размерности, такая, что для всех i  и  j  справедливо равенство: c_ij = aa_ij

4.              Произведением матрицы   размерности  (nxm)  на матрицу  размерности  (mxp) называется матрица   размерности  (nxp) такая, что

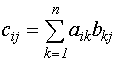                 (II.20)

5.              Матрица называется комплексно-сопряженной к  если в ней все матричные элементы a_ij  заменены на комплексно сопряженные a_ij^*. Матрица    называется транспонированной к  , если она получена заменой строк на столбцы и наоборот: a^’_ij = a_ji. Транспонированная и комплексно-сопряженная к  матрица называется сопряженной и обозначается

 

Любой квадратной матрице  можно поставить в соответствие определитель, обозначаемый как  det, который является суммой n!  членов, которыми служат всевозможные произведения n  матричных элементов a_ij, взятых по одному из строки и столбца.  Определитель обладает рядом интересных свойств:

а)   при транспонировании матриц определитель не меняется,

б) при перемене местами в матрице любых двух строк или столбцов местами он меняет свой знак на обратный,

в)   если в матрице два столбца или две строки равны между собой, то определитель равен нулю,

г)   если матрицы  и  квадратные, и = , то det=detdet                 (II.21).

 

Вернемся теперь к задачам квантовой механики. Как уже говорилось ранее, в квантовой механике особую важность имеют уравнения на собственные функции и собственные значения вида:

 

AY = aY                    (II.22)

 

Предположим, что нам известны решения другого уравнения на собственные значения: MФ_n = m_nФ_n  и тогда неизвестную функцию  Y  мы можем представить в виде ряда по известным функциям  {Ф_n}:    

 

Подставим теперь это разложение в   (II.22):

 

                (II.23)

 

Умножим теперь обе части на  Ф_n^* и проинтегрируем, учитывая ортонормированность функций Ф_n:  

 

 или

    (II.24)

 

Обозначим

 

  а  ,      (II.24)

 

тогда:

 

,  m =1, 2, 3, ....      (II.25)

 

Поскольку функции  {Ф_n}  известны, то известными можно считать и величины  , и поэтому систему уравнений  (II.25)  можно использовать для нахождения коэффициентов  {c_n}  и тем самым - функции  .  

 

В развернутом виде систему уравнений  (II.25)  можно записать как

 

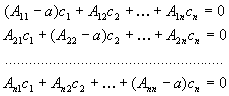      (II.26)

 

Из линейной алгебры известно, что эта система уравнений имеет нетривиальные решения только тогда, когда детерминант

 

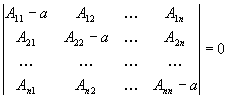      (II.27)

 

Раскрывая этот детерминант и решая его относительно параметра a,  подставляя затем результат в  (II.26), мы можем определить все коэффициенты разложения {c_m} и тем самым - неизвестную функцию  .

 

На этом мы можем считать законченным знакомство с основными, чисто математическими особенностями аппарата квантовой механики и вернутся к способам рассмотрения реальных физических ситуаций. Выше говорилось, что состояние микрообъекта можно описать путем задания волновой функции, а далее мы довольно много говорили об основах операторного исчисления. Естественно, нас интересует, естественно, не операторы как абстрактные математические объекты, а реальные физические величины, которые можно измерить в ходе эксперимента. Поэтому давайте вспомним

 

 

Необходимо отметить, что между операторами, как правило, сохраняются те же соотношения, которые имеют место между физическими величинами и в классической механике.

 

Для некоторых простейших и важнейших физических величин операторы можно выписать без всякого труда:

 

координата                     x ® x=x
время                             t ® t=t
составляющая импульса   px ® px=ihd/dx	(II.28)
кинетическая энергия  T=p2/2m ® h2/2m(d2/dx2+d2/dy2+d2/dz2)

 

Окончательную же связь между физическими величинами и соответствующими операторами можно установить на основе

 

                                                                                       (II.29)

 

                                                                                        (II.30)

 

Эти два положения можно скомбинировать, предположив, что

 

                 (II.31),

где  c_n  - некоторые коэффициенты, и тогда среднее значение величины  L  будет равно:

 

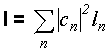                                  (II.32)

 

другими словами, величина  есть вероятность того, что в момент измерения наблюдаемой величины  L  будет получено значение , соответствующее волновой функции  уравнения на собственные значения (II.29).

 

Необходимо сформулировать и еще одно важнейшее свойство:

 

 

Это положение устанавливает связь математического аппарата квантовой механики с одним из основополагающих ее принципов - принципом неопределенности Гейзенберга и имеет очень большое значение при проведении каких-либо расчетов, поскольку из него следует, что коммутирующие операторы имеют общую систему собственных функций, что безусловно упрощает процедуры получения волновых функций сложных операторов.

 

Выше мы приводили операторы, соответствовавшие основным физическим величинам. Однако известно, что часто микрообъекты дополнительно характеризуются величинами, не имеющими аналогов в классической механике. Примером такой величины может быть спин, который не зависит ни от координат, ни от импульсов. Спину соответствует оператор спина  S  и операторы проекций на оси координат, для которых справедливы коммутационные соотношения:

 

s_xs_y-s_ys_x=ihs_z

s_ys_z-s_zs_y=ihs_x                                         (II.33)

s_zs_x-s_xs_z=ihs_y

 

Позднее мы будем рассматривать операторы спина более подробно.