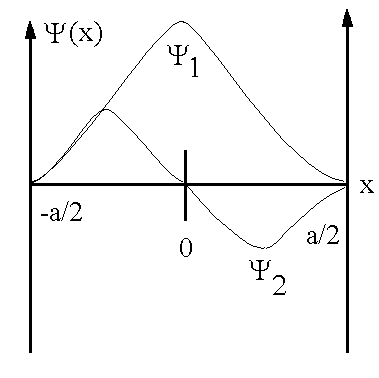Глава I.3.
Уравнение
Шредингера
Основной
задачей квантовой химии является нахождение решения уравнения на собственные
значения вида
LY
= lY (III.1)
для
различных операторов. Для ряда операторов - таких, как, например, оператор
проекции импульса, эти решения выписываются сразу. Действительно, в этом случае
уравнение (III.1) принимает вид:
-ihdY/dx
= pxY (III.2)
и
нетрудно убедится, что оно удовлетворяется функцией
Y
= const·exp(i/hpxx) (III.3)
где px
- постоянная, причем спектр ее значений неограничен: -µ < px
< +µ. Функция вида (III.3) обладает всеми свойствами волновой функции - она однозначна,
непрерывна и нормирована, так что на собственные значения px в данном
случае не накладывается никаких ограничений.
Для
некоторых операторов нахождение собственных функций хотя и несложно, однако
требует дополнительных рассуждений. Рассмотрим, например, оператор спина
электрона. Как уже говорилось, спин не имеет классического аналога, однако
известно, что для электрона он принимает следующие проекции на выделенную ось
(положим, z): +1/2h и -1/2h. С другой стороны известно, что
матрица оператора в своем собственном представлении диагональная и на диагонали
содержит собственные значения, поэтому матрица оператора проекции спина на ось z в своем собственном представлении
будет иметь вид:
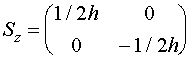 (III.4)
(III.4)
А из (III.4) с
учетом коммутационных свойств (II.33) мы можем получить и явный вид операторов
проекции спина на другие оси:
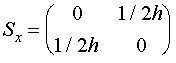 ,
, 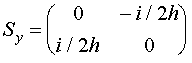 (III.5)
(III.5)
Теперь
попытаемся найти собственные функции этих операторов, положим ![]() . Поскольку он имеет только два собственных значения, то он
будет иметь и две собственные функции. Собственную функцию с собственным
значением +1/2h будем в дальнейшем полагать a,
а с собственным значением -1/2h - b,
так, что
. Поскольку он имеет только два собственных значения, то он
будет иметь и две собственные функции. Собственную функцию с собственным
значением +1/2h будем в дальнейшем полагать a,
а с собственным значением -1/2h - b,
так, что
![]() ,
, ![]() (III.6)
(III.6)
Далее,
поскольку ![]() есть матрица (2х2),
то из правил матричного умножения следует, что собственные функции a и b будут вектор-столбцами, причем
есть матрица (2х2),
то из правил матричного умножения следует, что собственные функции a и b будут вектор-столбцами, причем
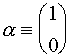 и
и 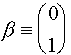 (III.7)
(III.7)
Нужно
убедится, что функции (III.7)
действительно являются собственными для оператора проекции спина, т.е.
удовлетворяют уравнениям (III.6) и для них выполняются все
требования, предъявляемые к волновым функциям, в частности, нормированность и
ортогональность. Однако, из всех операторов, встречающихся в квантовой
механике, основным является оператор Гамильтона, гамильтониан, который вводится
по аналогии с функцией Гамильтона в классической механике:
![]() (III.8)
(III.8)
(где
![]() ) и определяет значение полной энергии системы, из чего
следует его особая важность. В случае, когда гамильтониан явно не зависит от
времени, задача о его собственных функциях и собственных значениях сводится к
уравнению
) и определяет значение полной энергии системы, из чего
следует его особая важность. В случае, когда гамильтониан явно не зависит от
времени, задача о его собственных функциях и собственных значениях сводится к
уравнению
HY
= EY (III.9)
которое
называется стационарным уравнением Шредингера.
Так как E в этом уравнении
ожидаемое значение полной энергии, а оператор H коммутирует с большинством
операторов (координаты, импульса, момента импульса, квадрата момента импульса и
др.) и, следовательно, имеет с ними систему собственных функций, то решение
уравнения (III.9) означает практически полное описание всех параметров
физической системы.
Рассмотрим
теперь основные подходы к решению стационарного уравнения Шредингера для ряда
простейших модельных систем.
1. Свободное одномерное
движение частицы, т.е. частица находится в поле с постоянным
потенциалом и ее потенциальная энергия равна нулю. В этом случае уравнение (III.9) примет вид:
![]() , (III.10)
, (III.10)
или,
после несложных преобразований,
![]() , (III.11)
, (III.11)
где ![]() - некоторая
постоянная. Решением такого дифференциального уравнения (дифференциальное
уравнение второго порядка с постоянными коэффициентами) хорошо известно и в
общем случае имеет вид:
- некоторая
постоянная. Решением такого дифференциального уравнения (дифференциальное
уравнение второго порядка с постоянными коэффициентами) хорошо известно и в
общем случае имеет вид:
![]() , (III.12)
, (III.12)
где
![]() и
и ![]() - произвольные
постоянные. Легко убедится, что в данном случае на E не накладывается никаких
ограничений и энергетический спектр непрерывен.
- произвольные
постоянные. Легко убедится, что в данном случае на E не накладывается никаких
ограничений и энергетический спектр непрерывен.
Теперь
несколько усложним задачу и рассмотрим
2. Движение частицы в яме
с бесконечно высокими стенками. В этом случае потенциальная энергия будет равна
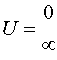
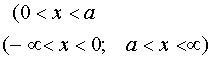 (III.13)
(III.13)
где
а - ширина потенциальной ямы.
Уравнение Шредингера (III.9) разобьется на два: для интервала x<0
и x>a и примет вид:
![]() , (III.14)
, (III.14)
и
может быть удовлетворено лишь функцией ![]() , т.е. частица не может находится за пределами потенциальной
ямы. Для интервала 0<x<a уравнение
Шредингера будет идентично (III.11), но с граничными условиями
, т.е. частица не может находится за пределами потенциальной
ямы. Для интервала 0<x<a уравнение
Шредингера будет идентично (III.11), но с граничными условиями
![]() (III.15)
(III.15)
Решением
уравнения (III.11) при дополнительных условиях (III.15) будет
функция (III.12), однако
константы ![]() и
и ![]() будут уже не
произвольными, а принимать вполне определенные значения: из условия
будут уже не
произвольными, а принимать вполне определенные значения: из условия ![]() следует
следует
![]() (III.16)
(III.16)
это
возможно только когда
![]()
Рассмотрим
теперь второе граничное условие - ![]() :
:
![]() (III.17)
(III.17)
или
![]()
Представим
теперь экспоненту в виде тригонометрических функций согласно формуле Эйлера:
![]() (III.18)
(III.18)
(необходимо
помнить, что![]() )
)
Приведя
подобные, мы это уравнение сведем к виду
![]() , где
, где ![]() (III.19)
(III.19)
Равенство (III.19)
справедливо при условии
![]() , или
, или ![]() (III.20)
(III.20)
где
n
- любое целое число.
Итак,
волновая функция частицы в потенциальной яме принимает вид
![]() (III.21)
(III.21)
С
другой стороны, из
![]() (III.22)
(III.22)
следует,
что энергия частицы может принимать следующие значения:
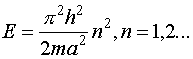 (III.23)
(III.23)
т.е.
энергия частицы является дискретной.
|
|
График волновых функций частицы в потенциальной яме для двух низших
значений n=1,2 |
3. Рассмотрим теперь
одномерное движение частицы по оси x
под воздействием упругой возвращающей силы ![]() , где k - силовая постоянная. Такая система
называется линейным гармоническим осциллятором.
, где k - силовая постоянная. Такая система
называется линейным гармоническим осциллятором.
Положим
для определенности ![]() , где
, где ![]() - частота колебаний,
можно записать уравнение Шредингера для линейного гармонического осциллятора:
- частота колебаний,
можно записать уравнение Шредингера для линейного гармонического осциллятора:
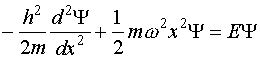 (III.24)
(III.24)
Если
ввести обозначения ![]() и
и ![]() , то (III.24) примет вид:
, то (III.24) примет вид:
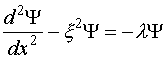 (III.25)
(III.25)
Непосредственно
найти решения этого уравнения нельзя, поэтому предположим, что ![]() , (это справедливо, когда амплитуда колебаний не велика). В
этом случае (III.25) перейдет в уравнение
, (это справедливо, когда амплитуда колебаний не велика). В
этом случае (III.25) перейдет в уравнение
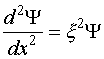 (III.26)
(III.26)
которое
имеет решения вида ![]() . Однако поскольку волновая функция должна быть ограниченной,
то физический смысл имеет только экспонента с отрицательным показателем:
. Однако поскольку волновая функция должна быть ограниченной,
то физический смысл имеет только экспонента с отрицательным показателем:
![]() (III.27)
(III.27)
Подстановка
этой функции в исходное уравнение (III.25) дает
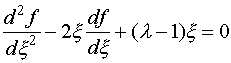 (III.28)
(III.28)
При
четных значениях величины ![]() ,
, ![]() это уравнение есть
хорошо известное уравнение Эрмита, решениями которого для n=0,1,2...
являются функции
это уравнение есть
хорошо известное уравнение Эрмита, решениями которого для n=0,1,2...
являются функции ![]() , называемыми полиномами Эрмита. Для низших n полиномы Эрмита имеют вид:
, называемыми полиномами Эрмита. Для низших n полиномы Эрмита имеют вид:
![]()
![]()
![]() (III.29)
(III.29)
![]()
.........................................
а
для собственных функций и собственных значений гармонического осциллятора мы
получим выражения:
![]() (III.30)
(III.30)
![]() (III.31)
(III.31)
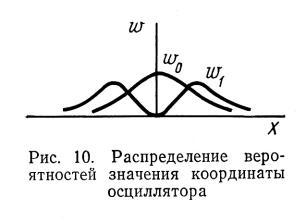
|
|
Графики волновых функций и соответствующие собственные значения для
низших n для линейного
гармонического осциллятора |
Интересно
отметить следующие особенности: система энергетических уровней дискретна с
постоянным интервалом, равным ![]() . Минимальная энергия, соответствующая нулевому уровню
составляет
. Минимальная энергия, соответствующая нулевому уровню
составляет ![]() . Состояние с нулевой энергий отсутствует, и это есть
следствие соотношения неопределенностей, так как если частица будет находиться
на самом дне потенциальной ямы, то это будет означать, что ее координата и
импульс одновременно точно определены, что невозможно.
. Состояние с нулевой энергий отсутствует, и это есть
следствие соотношения неопределенностей, так как если частица будет находиться
на самом дне потенциальной ямы, то это будет означать, что ее координата и
импульс одновременно точно определены, что невозможно.
Следует
также подчеркнуть, что модель гармонического осциллятора довольно широко
используется для описания колебательного движения ядер в молекулах, и,
следовательно, для отнесения
ИК-спектров.