Глава I.9.

 

Метод Хюккеля

 

Решение уравнения Хартри-Фока-Рутаана (XI.1) методом самосогласованного поля (ССП), рассмотренного в предыдущей главе, без использования каких-либо других приближений, лежит в основе неэмпирических методов расчета, которые отличаются используемым базисом атомных орбиталей .

 

      (XI.1)

 

При использовании данных методов основные затраты машинного времени (обычно около 70% всего требуемого для полного расчета времени) направлены на вычисление интегралов межэлектронного взаимодействия  и  оператора Фока

 

      (XI.2).

По мере увеличения размеров молекулы число таких интегралов возрастает примерно пропорционально , где N – размер базиса атомных орбиталей. Соответственно этому растут время и стоимость расчета.

 

Возможны два различных подхода, направленных на уменьшение вычислительных трудностей. Первый из них связан с пренебрежением части интегралов, входящих в выражение (XI.1), и сохранении во всем остальном неэмпирического расчета. Этот подход реализован в методе PRDDO (Partial Retention of Diatomic Differential Overlap), в котором сохраняются одно-, двух- и трехцентровые кулоновские интегралы и одно- и двухцентровые обменные интегралы. Фактически из всех  интегралов остаются  интегралов. Метод PRDDO, предложенный У. Липскомом с сотрудниками в 1973 г., по точности лишь немного уступает неэмпирическим расчетам в базисе STO-3G (В этом базисе каждая атомная орбиталь, представленная виде орбитали Слетера (VII.18), аппроксимируется тремя гауссовскими функциями

 

      (XI.3),

 

где  - нормировочный множитель,  – варьируемый параметр. Этот базис является минимальным, но достаточно удовлетворителен для воспроизведения молекулярной геометрии: ошибки в длинах связей 0.003 нм и углов ~4°).

 

Другой подход, оказавшийся более перспективным, основан на замене большей части интегралов параметрами, взятыми из эксперимента (потенциалами ионизации атомов в орбитальных валентных состояниях и др.), и использовании различных приближенных выражений, включающих параметры, для оценки интегралов. Основанные на этом подходе методы называются полуэмпирическими.

 

Самостоятельную область квантовой химии представляет теория электронного строения соединений с кратными связями (ненасыщенные системы). При расчете ненасыщенных систем обычно используют ,-приближение.

 

-Электронное приближение основано на предположении, что при квантово-механических расчетах ненасыщенных и ароматических соединений явно учитывается лишь система -электронов. Остальные электроны молекулы, к которым принадлежат и валентные -электроны, рассматриваются как жесткий скелет, в электростатическом поле которого движутся -электроны, и предполагаются не зависящими от изменений в -электронной системе. В полуэмпирических методах влияние этих электронов учитывается либо подбором параметров, либо формой потенциала. Эта идея была предложена немецким ученым Е. Хюккелем в 1931 г.

 

Строго говоря, с учетом неразличимости электронов следовало бы говорить не о - или -электронах, а о - и -состояниях, описываемых волновыми функциями соответствующей симметрии. Однако, такие понятия, как «-электроны», стали настолько привычными, что их можно рассматривать как современные квантово-химические термины.

 

Определение симметрии - и -состояний основано на том, что в плоских многоатомных молекулах можно подразделять атомные орбитали, образующие базис для представления молекулярных орбиталей, на две резко отличающиеся группы. К одной из них следует отнести -орбитали, которые антисимметричны относительно отражения в плоскости молекулы, а ко второй – -орбитали, симметричные по отношению к этому отражению. Например, в молекуле этилена, атомы которой лежат в плоскости xy, в минимальном базисе атомных орбиталей можно выделить орбитали (2p_z)₁ и (2p_z)₂, локализованные на атомах углерода молекулы, и эти орбитали обладают симметрией -типа. Остальные орбитали из указанного базиса обладают симметрией -типа. Атомные -орбитали образуют базис для построения молекулярных -орбиталей, которые используются для описания -связей. В молекуле этилена имеются два -электрона (одна двойная связь), бензол имеет шесть -электронов и т.д.

 

В приближении Хартри-Фока, фокиан F для невырожденных электронных состояний полносимметричен, что означает, что матричные элементы фокиана на орбиталях разного типа симметрии согласно теореме Вигнера-Эккарта должны быть равны нулю. Если базис, в котором представлены молекулярные орбитали, разбит на два базисных набора (или может быть сведен к таким наборам) симметричных и антисимметричных функций, то матричные элементы фокиана  будут равны нулю, если  и  разного типа симметрии, и будут отличны от нуля в противном случае. Это означает, что матрица фокиана, как и матрица интегралов перекрывания, имеет блочно-диагональный вид

 

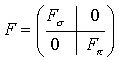      (XI.4).

 

И хотя матричные элементы в каждом блоке за счет двухэлектронных интегралов зависят от всего набора орбиталей – и , и , тем не менее, задачу можно решать итерациями, сначала определяя -орбитали, затем – -орбитали, затем вновь возвращаясь к определению -орбиталей и т.п. Если же считать -орбитали приближенно известными на основе модельных представлений, то можно в конечном итоге ограничиться рассмотрением лишь -блока.

 

-Электроны отличаются от -электронов не только свойствами симметрии. Прежде всего, каждая группа электронов движется в различных частях молекулы. -Электроны имеют равную нулю вероятность нахождения в плоскости молекулы, в то время как -электроны имеют максимальную вероятность нахождения в этой плоскости. -Электроны обычно связаны с молекулой слабее, чем -электроны, так что они более поляризованы, легче ионизируются и обладают большей реакционной способностью, а поэтому в большей мере ответственны за химические и физические свойства -электронных соединений (электронные спектры, потенциалы ионизации и т.д.). Кроме этого, состояния -электронов можно локализовать в пространстве, и поэтому их можно отнести к связям между парами соседних атомов либо к «неподеленным» электронным пара на отдельных атомах, в то время как -электроны образуют делокализованную систему в области сопряженного скелета молекулы.

 

В методе молекулярных орбиталей Хюккеля (МОХ) полностью пренебрегают интегралами межэлектронного отталкивания. При этом условии матричные элементы фокиана совпадают с матричными элементами остова:

 

    =>    ,    при условии     и .

В то же время остовые интегралы параметризуются:

 

 

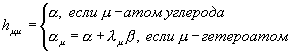
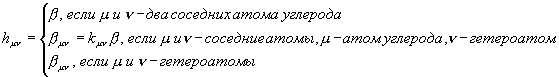
Величины параметров ( и др.) определяются из эксперимента. Если требуется провести расчет каких-то конкретных характеристик, например дипольных моментов группы соединений, включающих, допустим, sp²-гибридизованный азот в системе сопряженных связей, проводят расчеты нескольких стандартных соединений, варьируя параметры, и выбирают затем те из них, которые лучше воспроизводят экспериментальные значения. С этими параметрами рассчитывают затем остальные соединения.

 

Такой способ оценки приводит неизбежно к большому числу разных параметров, которые могут зависеть от характеристики, используемой для их выбора. Однако для стандартизации можно воспользоваться обоснованными общими соображениями об относительных значениях параметров.

 

 – кулоновский интеграл sp²-углеродного атома, достаточно хорошей оценкой которого является потенциал ионизации электрона, находящегося на атомной орбитали изолированного атома;

 – резонансный интеграл стандартной связи C-C, величина которого обычно принимается равной –2.318 эВ;

 – резонансный интеграл связи двух атомов (в одном случае, первый – атом углерода, а второй – гетероатом, в другом случае, оба атома относятся к разным элементам). Для его определения в простейшем случае необходимо знать  (безразмерная величина), хотя, вообще говоря, следует рассматривать зависимость интегралов от длины связей. Для этого предложено несколько эмпирических формул (табл.1). Эти формулы не имеют строго обоснованного вывода. Они были подобраны эмпирическим путем, так как давали результаты, сравнимые с экспериментальными данными.

 

Табл.1. Эмпирические формулы для расчета резонансных интегралов.

 

 – безразмерная величина, для связи C-X (C – атом углерода, X – гетероатом) в простейшем случае равная разности электроотрицательностей по Полингу этих двух элементов:

      (XI.5), где  – электроотрицательность элемента.

Из многих систем параметров наибольшее распространение получил набор параметров Стрейтвизера, который может быть рекомендован для большинства случаев, где расчет по методу Хюккеля целесообразен. В табл.2 приведены параметры для наиболее часто встречаемых атомов и их валентных состояний.

 

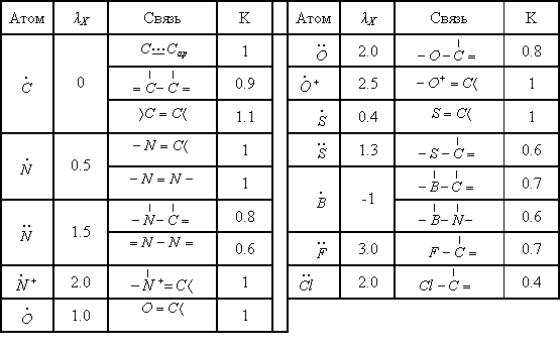
Табл.2. Параметры гетероатомов и образуемых ими связей, применяемые в методе МОХ.

Примечание: связь  характерна для соединений с протонированной карбонильной группой.

 

Интегралы перекрывания в уравнении (XI.1) заменяются символом Кронекера:

 

      (XI.6)

 

Молекулярные орбитали формируются только 2p_z-атомными орбиталями:

 

      (XI.7),

где  – 2p_z-орбиталь i атома.

 

 

 

Пример решения задачи

 

Определить вид волновых функций и энергии соответствующих молекулярных орбиталей молекулы формальдегида

.

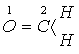Волновая функция будет иметь вид

      (XI.8).

 

Задача состоит в нахождении коэффициентов c_kC и c_kO атомных орбиталей и энергии  молекулярных орбиталей, определяемых решением системы линейных однородных уравнений:

 

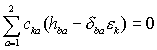      (XI.9).

Соответствующее секулярное уравнение записывается как

 

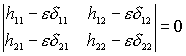      (XI.10).

 

Учитывая приближение метода Хюккеля, можно переписать это уравнение в виде

 

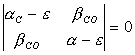      (XI.11).

Введем обозначения  (XI.12) и  (XI.13) и разделим каждую строку определителя на .

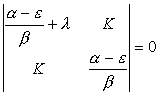      (XI.14).

Введем обозначение  (XI.15). Тогда секулярное уравнение примет вид

 

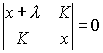      (XI.16).

Из табл.2 берем значения K и

 

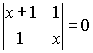    (XI.17).

Корни этого уравнения: x₁=-1.618, x₂=0.618. Соответственно, значения энергий молекулярных орбиталей равны:

      (XI.18).

Определим теперь коэффициенты c_kC и c_kO. Перепишем детерминант (XI.17) в виде системы линейных уравнений и учтем условие :

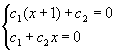      (XI.19).

 

Решение этой системы приводит к молекулярным орбиталям вида:

 

      (XI.20).

 

 

 

Характеристики молекул, определяемые значениями энергий молекулярных орбиталей и коэффициентами атомных орбиталей в МО

 

Для описания распределения электронной плотности в молекулах необходимо использовать формулы для нахождения электронной плотности на атоме и порядка связи между атомами.

 

Полная электронная плотность, создаваемая -электронами сопряженной молекулы, равна в приближении ЛКАО МО:

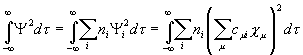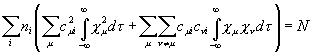=    (XI.21),

где n_i – число электронов на i-ой молекулярной орбитали; N – общее число -электронов в молекуле. Коэффициенты предполагаются действительными. При условии ортонормированности атомных орбиталей  и , принимаемом в методе МОХ, двойная сумма обращается в нуль, и выражение (XI.21) сводится к сумме:

 

      (XI.22).

Каждую сумму в этом выражении можно приближенно рассматривать как вклад электронов, находящихся на орбитали -го атома, в полную электронную плотность. Соответственно выражение

 

    (XI.23)

называют электронной плотностью на -м атоме.

 

Величину

 

    (XI.24)

называют порядком связи между атомами  и . Эти члены возникают как коэффициенты при интегралах перекрывания в двойной сумме (XI.21) и вследствие ортонормированности атомных орбиталей исчезают вместе с интегралами перекрывания. Выражение (XI.24) предполагает все же, что, если произведение  достаточно велико (и положительно), существует значительная вероятность найти электрон i-ой молекулярной орбитали в пространстве между атомами  и .

 

Через величины (XI.23) и (XI.24) определяется матрица плотности первого порядка

 

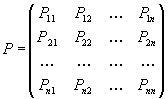      (XI.25),

которая и описывает распределение электронной плотности в молекуле.

 

Данная матрица позволяет вычислить любое одноэлектронное свойство того состояния системы, к которому она относится. Если обозначить это свойство , то его среднее значение равно следу произведения матриц P и  ( является оператором, который в матричном виде представляется как ):

      (XI.26).

Заряд атома определяется выражением

      (XI.27),

где  – число электронов, вносимых атомом  в общую -систему.

 

В методе молекулярных орбиталей Хюккеля не учитывается отталкивание между электронами на различных МО, поэтому полную энергию молекулы можно представить в виде суммы энергий отдельных электронов:

 

      (XI.28).

Самым простым способом оценки ароматичности является расчет энергии делокализации DE, или энергии резонанса. Это разность между полной электронной энергией молекулы и энергиями изолированных двойных связей, включенных в состав молекулы. Она характеризует выигрыш в энергии за счет делокализации -электронов.

 

Примером может служить молекула бензола. Ее полная энергия равна , энергия молекулы этилена  (соответственно энергия трех молекул этилена ). Разница составляет , следовательно, .

 

 

 

Расширенный метод Хюккеля

 

Расширенный метод Хюккеля (РМХ) был введен в практику в 1963 г. Хоффманом. В этом методе, как и в простом методе Хюккеля (МОХ), пренебрегают всеми интегралами межэлектронного взаимодействия, а отличие заключается в следующем:

1.      В то время как в методе МОХ в базис для разложения МО включают только p_z-орбитали атомов углерода, в методе РМХ учитываются все атомные орбитали валентных электронов, например 1s-орбитали для водорода, 2s-, 2p_x-, 2p_y и 2p_z-орбитали для углерода и т.п.

2.      Диагональные матричные элементы  полагаются равными потенциалам ионизации соответствующих валентных электронов, взятых с обратным знаком (табл.3):

3.      Для вычисления недиагональных матричных элементов предложено несколько формул:

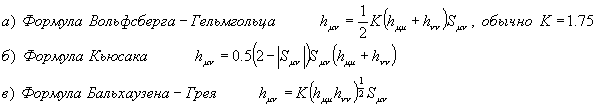
Эти формулы (как и формулы в таб.1) не имеют строгого вывода, а подобраны эмпирически.

4.      Интегралы перекрывания  вычисляют исходя из задаваемой геометрии молекулы.

 

Табл.3. Ионизационные потенциалы валентных состояний электронов для некоторых атомов второго и третьего периодов (эВ).

 

Полная энергия молекулы с заполненной электронной оболочкой вычисляется как удвоенная сумма энергий занятых МО:

      (XI.29).

 

Вследствие неучета в явном виде межэлектронного и межъядерного взаимодействия РМХ плохо предсказывает равновесные длины связей даже для молекул с равномерным распределением заряда по атомам, поэтому для оптимизации длин связей РМХ практически не применяется. Для молекул с неравномерным распределением заряда РМХ приводит к существенным ошибкам и в определении геометрической конфигурации. В то же время РМХ, несомненно, очень быстрое и экономное средство для оценки относительной устойчивости конформеров молекул со слабо поляризованными связями. Кроме того, чрезвычайно важной положительной стороной РМХ является довольно точное воспроизведение им относительного порядка энергетических уровней и строения молекулярных орбиталей молекул со слабой поляризацией связей.